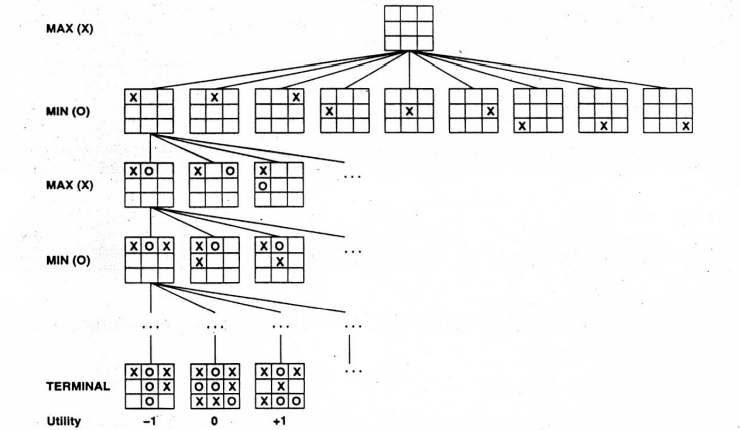
📗 The search problem for games (one or more opponents are searching at the same time) is adversarial search: Link, Wikipedia.
➩ The initial state is the beginning of the game.
➩ Each successor represent an action or a move in the game.
➩ The goal states are called terminal states, the search problem tries to find the terminal state with the lowest cost (highest reward).
📗 The opponents search at the same time and tries to minimize their costs (or maximize their rewards).
➩ For zero-sum games, the sum of the rewards and costs for the two players is 0 at every terminal state. The opponent minimizes the reward (or maximizes the cost) of the first agent: Wikipedia.
TopHat Discussion
📗 [1 points] pirate got gold coins. Each pirate takes a turn to propose how to divide the coins, and all pirates who are still alive will vote whether to (1) accept the proposal or (2) reject the proposal, kill the pirate who is making the proposal, and continue to the next round. Use strict majority rule for the vote, and use the assumption that if a pirate is indifferent, they will vote reject with probability 50 percent. How will the first pirate propose? Enter a vector of length , all integers, sum up to .
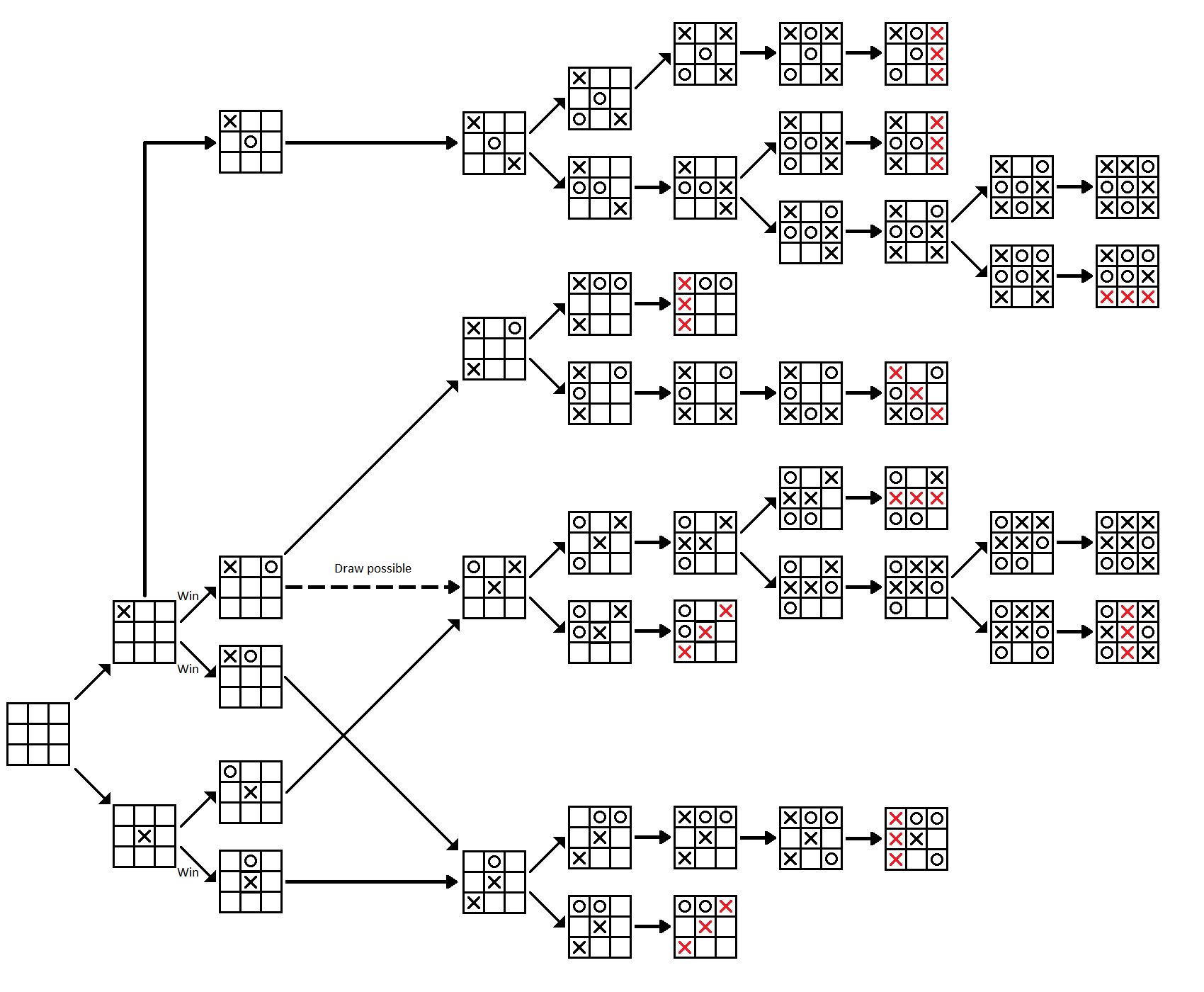
📗 DFS on the game tree is called the minimax algorithm: Link, Wikipedia.
➩ The game is solved backward starting from the terminal states.
➩ Each agent (player) chooses the best action given the optimal actions of all players in the subtrees (subgames).
📗 For zero-sum games, the optimal value at an internal state for the MAX player is called \(\alpha\left(s\right)\) and for the MIN player is called \(\beta\left(s\right)\).
📗 The time and space complexity is the same as DFS with \(D = d\).
TopHat Discussion
📗 [4 points] Highlight the nodes that will be alpha-beta pruned in the following game.
📗 For non-deterministic games, some internal states represent moves by Chance (can be viewed as another player), for example, dice roll or coin flip. For those states, expected cost or reward are used instead of max or min.
📗 DFS on games with Chance is called expectiminimax: Wikipedia.
TopHat Quiz
(Past Exam Question) ID:
📗 [4 points] Consider a zero-sum sequential move game with Chance. player moves first, then Chance, then . The values of the terminal states are shown in the diagram (they are the values for the Max player). What is the (expected) value of the game (for the Max player)?
📗 Note: in case the diagram is not clear, the probabilities from left to right is: , and the rewards are .
📗 When a branch will not lead the current agent (player) to win, the branch can be pruned (both players will not need to search the subtree). DFS with pruning is called Alpha-Beta Pruning: Wikipedia.
➩ During DFS, keep track of both \(\alpha\left(s\right)\) and \(\beta\left(s\right)\) for each state.
➩ Prune the subtree after \(s\) if \(\alpha\left(s\right) \geq \beta\left(s\right)\).
TopHat Discussion
📗 [4 points] Highlight the nodes that will be alpha-beta pruned in the following game.
📗 The heuristic to estimate the value at an internal state for games is called a static (board) evaluation (SBE) function: Wikipedia.
➩ For zero-sum games, SBE for one player should be the negative of the SBE for the other player.
➩ At terminal states, the SBE should agree with the cost or reward at that state.
📗 For Chess, the SBE can be computed by a neural network based some features such as: material, mobility, king safety, center control; or a convolutional neural network treating the board as an image.
📗 IDS can be used with SBE.
➩ In iteration \(d\), the depth is limited to \(d\) and the SBE of the internal states at depth \(d\) are used as their cost or reward.
📗 Random subgames can be simulated by selecting random moves for both players: Wikipedia.
📗 The move corresponding to the highest expected reward (win rates) can be picked.
📗 The move corresponding to the highest upper confidence bound of the win rates can also be used: \(\dfrac{w_{s}}{n_{s}} + c \sqrt{\dfrac{\log T}{n_{s}}}\), where \(w\) is the number of wins after state \(s\), \(n\) is the number of simulations after \(s\), and \(T\) is the total number of simulations.
Example
📗 Alpha GO uses Monte Carlo Tree Search with more than \(10^{5}\) play-outs: Wikipedia.
📗 Alpha GO uses convolutional neural network to compute SBE: Link.
📗 Unlike sequential games, for simultaneous move games, one player (agent) does not know the action taken by the other player.
📗 Given the actions of the other players, the optimal action is called the best response.
📗 An action is dominated if it is worse than another action given all actions of the other players.
➩ For finite games, an action is dominated if and only if it is never a best response.
➩ An action is strictly dominated if it is strictly worse than another action given all actions of the other players. A dominated action is weakly dominated if it is not strictly dominated.
📗 A solution of a simultaneous move game is called an equilibrium.
➩ Rationalizability (IESDS, Iterative Elimination of Strictly Dominated Strategies): iteratively remove the actions are that dominated (never best responses): Wikipedia.
➩ Nash Equilibrium: mutual best responses: Wikipedia.
TopHat Discussion
📗 [1 points] Write down an integer between and that is the closest to two thirds \(\dfrac{2}{3}\) of the average of everyone's (including yours) integers.
📗 Answer: .
TopHat Quiz
(Past Exam Question) ID:
📗 [4 points] Perform iterated elimination of strictly dominated strategies (i.e. find rationalizable actions). Player A's strategies are the rows. The two numbers are (A, B)'s payoffs, respectively. Recall each player wants to maximize their own payoff. Enter the payoff pair that survives the process. If there are more than one rationalizable action, enter the pair that leads to the largest payoff for player A.
A \ B
I
II
III
I
II
III
IV
📗 Answer (comma separated vector): .
TopHat Quiz
(Past Exam Question) ID:
📗 [4 points] What is the row player's value in a Nash equilibrium of the following zero-sum normal form game? A (row) is the max player, B (col) is the min player. If there are multiple Nash equilibria, use the one with the largest value (to the max player).
📗 A symmetric simultaneous move game is a prisoner's dilemma game if the Nash equilibrium (using strictly dominant actions) is strictly worse for all players than another outcome: Link, Wikipedia.
➩ For two players, the game can be represented by a game matrix: \(\begin{bmatrix} - & C & D \\ C & \left(x, x\right) & \left(0, y\right) \\ D & \left(y, 0\right) & \left(1, 1\right) \end{bmatrix}\), where C stands for Cooperate (or Deny) and D stands for Defect (or Confess), and \(y > x > 1\). Here, \(\left(D, D\right)\) is the only Nash equilibrium (using strictly dominant actions) but \(\left(C, C\right)\) is strictly preferred by both players.
Example
📗 Split or Steal games: (YouTube playlist: Link, Solution: Link).
📗 A mixed strategy is when a player randomizes between multiple actions: Wikipedia.
📗 A pure strategy is when a player uses only one action with probability 1.
📗 A mixed strategy Nash equilibrium is a Nash equilibrium for the game in which mixed strategies are allowed.
➩ For example, for rock paper scissor games, there is no pure Nash equilibrium, but there is one mixed Nash equilibrium where every player uses each action with probability \(\dfrac{1}{3}\): Link.
TopHat Quiz
(Past Exam Question) ID:
📗 [4 points] Given the following game payoff table, suppose the row player uses a pure strategy, and column player uses a mixed strategy playing L with probability \(q\). What is the smallest and largest value of \(q\) in a mixed strategy Nash equilibrium?
Row \ Col
L
R
U
D
Note: the following is a diagram of the best responses (make sure you understand what they are and how to draw them). The red curve is the best response for the column player and the blue curve is the best response for the row player.
📗 Answer (comma separated vector): .
TopHat Quiz
(Past Exam Question) ID:
📗 [4 points] Suppose \(n\) = witnesses heard a gunshot near 221B Baker Street. The benefit from at least one witness calling the police is \(b\) = and the cost of calling the police is \(c\) = . If no witness calls the police, everyone gets 0. In a Nash equilibrium in which every witness uses the same mixed strategy, what is the probability that no one calls the police?