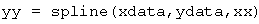Interpolating with cubic splines using Matlab

If you have a lot of data points then there is a way to interpolate the data with a low degree polynomial. To do this you only interpolate four points at once using a special cubic polynomial function called a cubic spline function. Imagine that you have 10 data points. The cubic spline function interpolates the first four data points (1-4) with a cubic polynomial. It then interpolates points (2-5) with another cubic polynomial and then interpolates points (3-6) with another, until it gets to points (7-10). The cubic spline function has the following properties:

1) between successive data points, 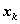and 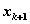S(x) is a cubic polynomial,
2) at each data point 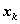, the first derivative S'(x) is continuous,
3) at each data point 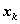the second derivative S''(x) is continuous.

These mathematical properties of the cubic spline function result in a very smooth curve that interpolates data points and does not wildly oscillate between data points, like a high degree polynomial does.

The Matlab function for evaluating the cubic spline function is called spline. If xdata and ydata are Matlab vector variables that contain data points, then spline function values that are evaluated at the interpolation points in the vector xx are given by