Prev: W10 Next: W12
Blank Slides (with blank pages for quiz questions): Part 1, Part 2,
Annotated Slides: Part 1, Part 2,
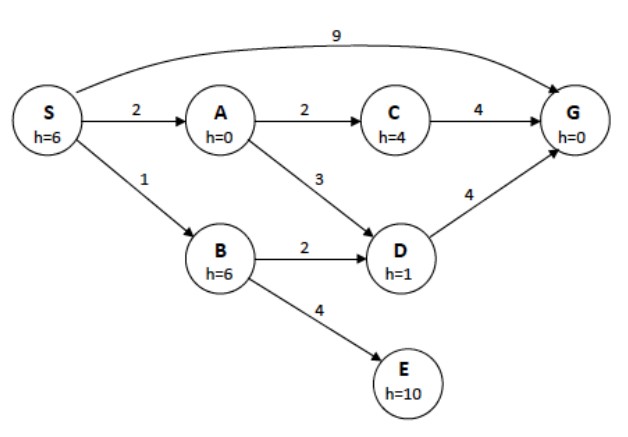
Image from Professor Dyer's CS540 lecture slides.
N/A
Part 2 (Simulated Annealing): Link
Part 3 (Genetic Algorithm): Link
SAT Solver: Link
Genetic Walkers: Link
Genetic Cars: Link
Genetic Eater: Link
Genetic Image: Link
# Summary
📗 Monday lecture: 5:30 to 8:30, Zoom Link
📗 Office hours: 5:30 to 8:30 Wednesdays (Dune) and Thursdays (Zoom Link)
📗 Personal meeting room: always open, Zoom Link
📗 Quiz (use your wisc ID to log in (without "@wisc.edu")): Socrative Link, Regrade request form: Google Form (select Q9).
📗 Math Homework:
M10,
📗 Programming Homework:
P5,
📗 Examples, Quizzes, Discussions:
Q9,
# Lectures
📗 Slides (before lecture, usually updated on Saturday):
Blank Slides:
Part 1,
Part 2,
Blank Slides (with blank pages for quiz questions): Part 1, Part 2,
📗 Slides (after lecture, usually updated on Tuesday):
Blank Slides with Quiz Questions:
Part 1,
Part 2,
Annotated Slides: Part 1, Part 2,
📗 My handwriting is really bad, you should copy down your notes from the lecture videos instead of using these.
📗 Notes

Image from Professor Dyer's CS540 lecture slides.
N/A
# Other Materials
📗 Pre-recorded Videos from 2020
Part 1 (Hill Climbing): Link Part 2 (Simulated Annealing): Link
Part 3 (Genetic Algorithm): Link
📗 Relevant websites
Simulated Annealing Map: Link SAT Solver: Link
Genetic Walkers: Link
Genetic Cars: Link
Genetic Eater: Link
Genetic Image: Link
📗 YouTube videos from 2019 to 2021
How to find reproduction probabilities? Link # Keywords and Notations
📗 Local Search
📗 Hill Climbing (Valley Finding), probability of moving from \(s\) to a state \(s'\) \(p = 0\) if \(f\left(s'\right) \geq f\left(s\right)\) and \(p = 1\) if \(f\left(s'\right) < f\left(s\right)\), where \(f\left(s\right)\) is the cost of the state \(s\).
📗 Simulated Annealing, probability of moving from \(s\) to a worse state \(s'\) = \(p = e^{- \dfrac{\left| f\left(s'\right) - f\left(s\right) \right|}{T\left(t\right)}}\) if \(f\left(s'\right) \geq f\left(s\right)\) and \(p = 1\) if \(f\left(s'\right) < f\left(s\right)\), where \(T\left(t\right)\) is the temperature as time \(t\).
📗 Genetic Algorithm, probability of get selected as a parent in cross-over: \(p_{i} = \dfrac{F\left(s_{i}\right)}{\displaystyle\sum_{j=1}^{n} F\left(s_{j}\right)}\), \(i = 1, 2, ..., N\), where \(F\left(s\right)\) is the fitness of state \(s\).
Last Updated: January 19, 2026 at 9:18 PM