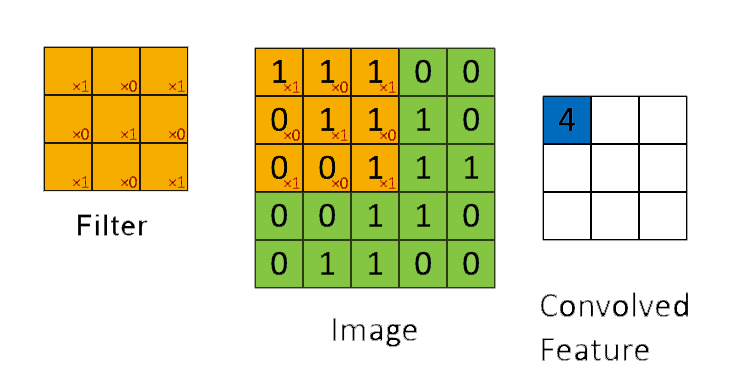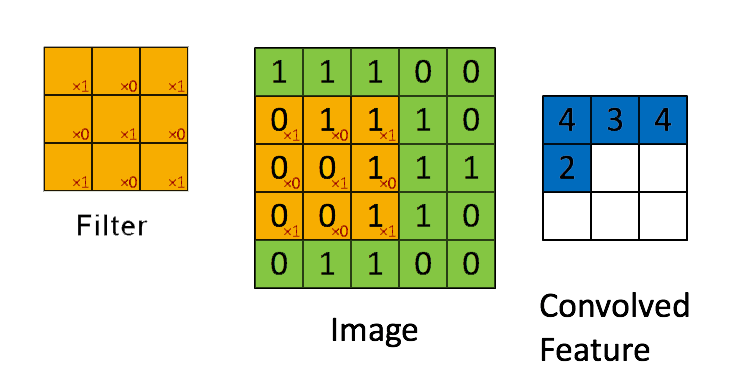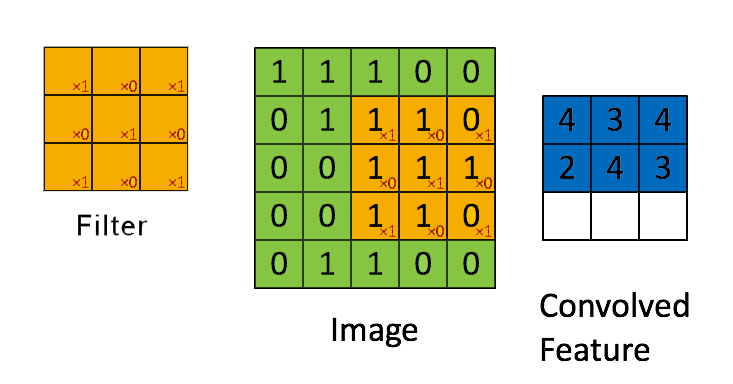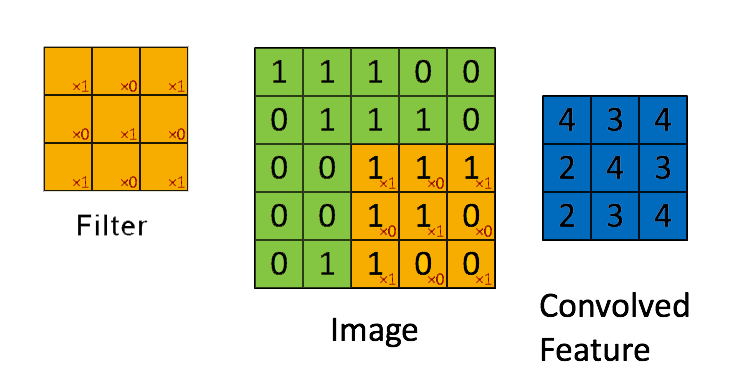
Prev: W4 Next: W6
Blank Slides (with blank pages for quiz questions): Part 1, Part 2,
Annotated Slides: Part 1, Part 2,
Part 2 (HMM Evaluation): Link
Part 3 (HMM Training): Link
Part 4 (Recurrent Neural Network): Link
Part 5 (Backprop Through Time): Link
Part 6 (RNN Variants): Link
LTSM and GRU: Link
How to generate realizations of discrete random variables using CDF inversion? Link
Example: How to compute the joint probability given the conditional probability table? Link
Example (Quiz): How to compute conditional probability table given training data? Link
Example (Quiz): How to do inference (find joint and conditional probability) given conditional probability table? Link
Example (Quiz): How to find the conditional probabilities for a common cause configuration? Link
Joint probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y \in Y} \mathbb{P}\left\{X = x, Y = y\right\}\).
Bayes rule: \(\mathbb{P}\left\{Y = y | X = x\right\} = \dfrac{\mathbb{P}\left\{X = x | Y = y\right\} \mathbb{P}\left\{Y = y\right\}}{\displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}}\).
Law of total probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}\).
Independence: \(X, Y\) are independent if \(\mathbb{P}\left\{X = x, Y = y\right\} = \mathbb{P}\left\{X = x\right\} \mathbb{P}\left\{Y = y\right\}\) for every \(x, y\).
Conditional independence: \(X, Y\) are conditionally independent conditioned on \(Z\) if \(\mathbb{P}\left\{X = x, Y = y | Z = z\right\} = \mathbb{P}\left\{X = x | Z = z\right\} \mathbb{P}\left\{Y = y | Z = z\right\}\) for every \(x, y, z\).
Conditional Probability Table estimation (with Laplace smoothing): \(\hat{\mathbb{P}}\left\{x_{j} | p\left(X_{j}\right)\right\} = \dfrac{c_{x_{j}, p\left(X_{j}\right)} + 1}{c_{p\left(X_{j}\right)} + \left| X_{j} \right|}\), where \(\left| X_{j} \right|\) is the number of possible values of \(X_{j}\).
Bayesian network inference: \(\mathbb{P}\left\{x_{1}, x_{2}, ..., x_{m}\right\} = \displaystyle\prod_{j=1}^{m} \mathbb{P}\left\{x_{j} | p\left(X_{j}\right)\right\}\).
Naive Bayes estimation: .
Naive Bayes classifier: \(\hat{y}_{i} = \mathop{\mathrm{argmax}}_{y} \mathbb{P}\left\{Y = y | X = X_{i}\right\}\).
# Summary
📗 Monday lecture: 5:30 to 8:30, Zoom Link
📗 Office hours: 5:30 to 8:30 Wednesdays (Dune) and Thursdays (Zoom Link)
📗 Personal meeting room: always open, Zoom Link
📗 Quiz (use your wisc ID to log in (without "@wisc.edu")): Socrative Link, Regrade request form: Google Form (select Q5).
📗 Math Homework:
M5,
📗 Programming Homework:
P2,
📗 Examples, Quizzes, Discussions:
Q5,
# Lectures
📗 Slides (before lecture, usually updated on Saturday):
Blank Slides:
Part 1,
Part 2,
Blank Slides (with blank pages for quiz questions): Part 1, Part 2,
📗 Slides (after lecture, usually updated on Tuesday):
Blank Slides with Quiz Questions:
Part 1,
Part 2,
Annotated Slides: Part 1, Part 2,
📗 My handwriting is really bad, you should copy down your notes from the lecture videos instead of using these.
📗 Notes
# Other Materials
📗 Pre-recorded Videos from 2020
Part 1 (Hidden Markov Model): Link Part 2 (HMM Evaluation): Link
Part 3 (HMM Training): Link
Part 4 (Recurrent Neural Network): Link
Part 5 (Backprop Through Time): Link
Part 6 (RNN Variants): Link
📗 Relevant websites
RNN Visualization: Link LTSM and GRU: Link
📗 YouTube videos from 2019 to 2021
How to find maximum likelihood estimates for Bernoulli distribution? Link How to generate realizations of discrete random variables using CDF inversion? Link
Example: How to compute the joint probability given the conditional probability table? Link
Example (Quiz): How to compute conditional probability table given training data? Link
Example (Quiz): How to do inference (find joint and conditional probability) given conditional probability table? Link
Example (Quiz): How to find the conditional probabilities for a common cause configuration? Link
# Keywords and Notations
📗 Probability Review:
Conditional probability: \(\mathbb{P}\left\{Y = y | X = x\right\} = \dfrac{\mathbb{P}\left\{Y = y, X = x\right\}}{\mathbb{P}\left\{X = x\right\}}\). Joint probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y \in Y} \mathbb{P}\left\{X = x, Y = y\right\}\).
Bayes rule: \(\mathbb{P}\left\{Y = y | X = x\right\} = \dfrac{\mathbb{P}\left\{X = x | Y = y\right\} \mathbb{P}\left\{Y = y\right\}}{\displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}}\).
Law of total probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}\).
Independence: \(X, Y\) are independent if \(\mathbb{P}\left\{X = x, Y = y\right\} = \mathbb{P}\left\{X = x\right\} \mathbb{P}\left\{Y = y\right\}\) for every \(x, y\).
Conditional independence: \(X, Y\) are conditionally independent conditioned on \(Z\) if \(\mathbb{P}\left\{X = x, Y = y | Z = z\right\} = \mathbb{P}\left\{X = x | Z = z\right\} \mathbb{P}\left\{Y = y | Z = z\right\}\) for every \(x, y, z\).
📗 Bayesian Network
Conditional Probability Table estimation: \(\hat{\mathbb{P}}\left\{x_{j} | p\left(X_{j}\right)\right\} = \dfrac{c_{x_{j}, p\left(X_{j}\right)}}{c_{p\left(X_{j}\right)}}\), where \(p\left(X_{j}\right)\) is the list of parents of \(X_{j}\) in the network. Conditional Probability Table estimation (with Laplace smoothing): \(\hat{\mathbb{P}}\left\{x_{j} | p\left(X_{j}\right)\right\} = \dfrac{c_{x_{j}, p\left(X_{j}\right)} + 1}{c_{p\left(X_{j}\right)} + \left| X_{j} \right|}\), where \(\left| X_{j} \right|\) is the number of possible values of \(X_{j}\).
Bayesian network inference: \(\mathbb{P}\left\{x_{1}, x_{2}, ..., x_{m}\right\} = \displaystyle\prod_{j=1}^{m} \mathbb{P}\left\{x_{j} | p\left(X_{j}\right)\right\}\).
Naive Bayes estimation: .
Naive Bayes classifier: \(\hat{y}_{i} = \mathop{\mathrm{argmax}}_{y} \mathbb{P}\left\{Y = y | X = X_{i}\right\}\).
Last Updated: January 19, 2026 at 9:18 PM