Prev: W4 Next: W6
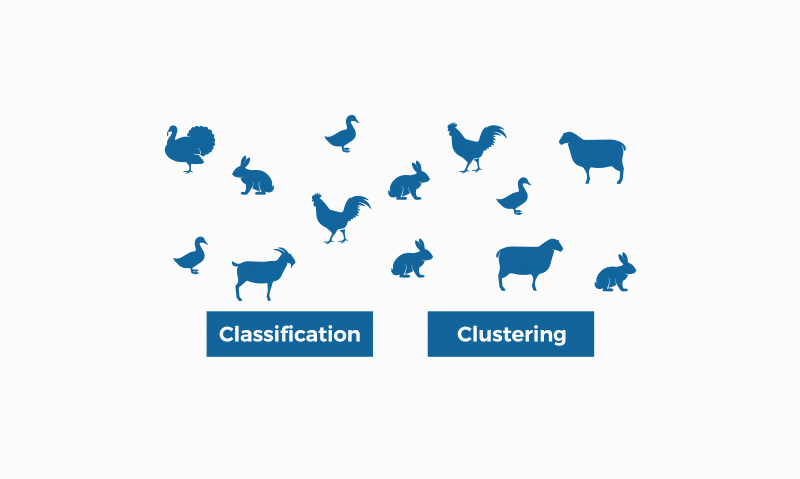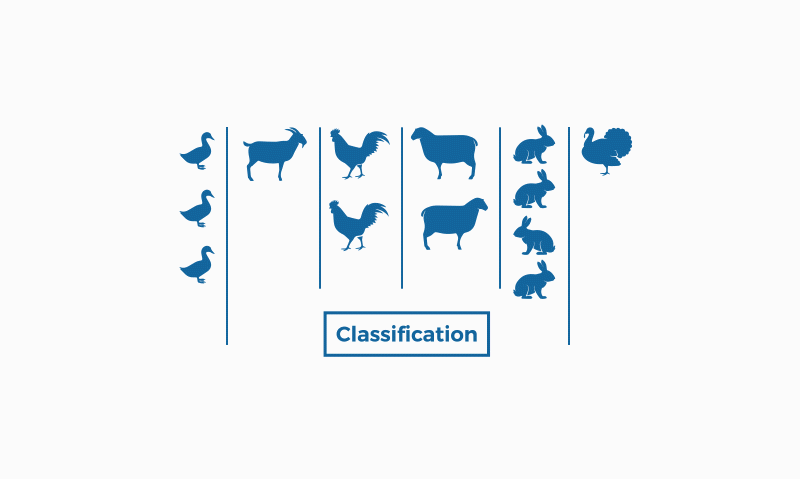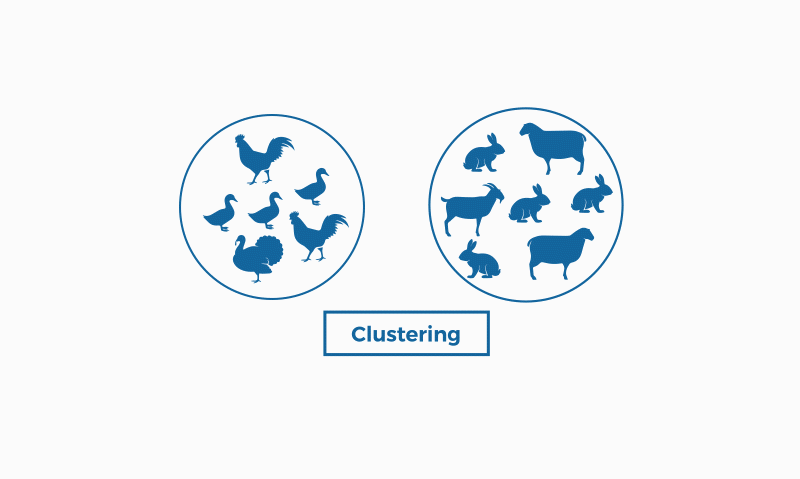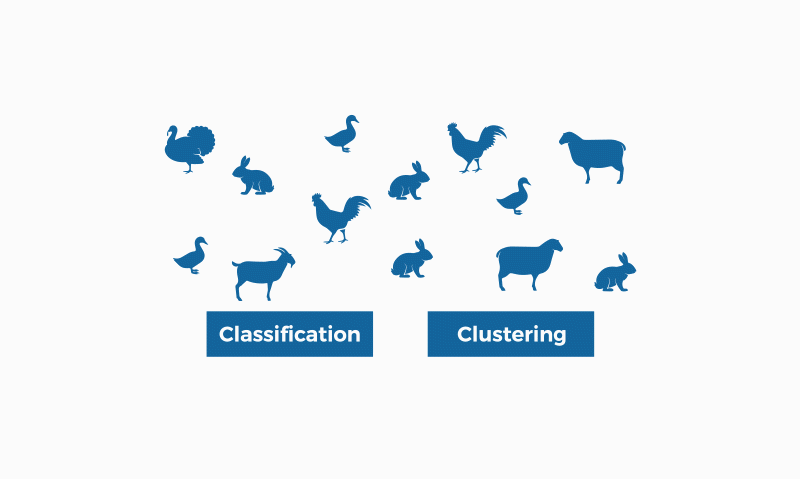
Image by bismart
Lecture 15 Part 2 (Hierarchical Clustering): Link
Lecture 15 Part 3 (K Means Clustering): Link
Lecture 16 Part 1 (Dimensionality Reduction): Link
Lecture 16 Part 2 (Principal Component): Link
Lecture 16 Part 3 (Non-linear PCA): Link
Hierachical Clustering: Link
Tree of Life: Link 1, Link 2
K Means Clustering: Link
K Gaussian Mixture: Link
Word Embedding: Link
Principal Component: Link
Eigen Face: Link 1, Link 2
t-distributed Stochastic Neighbor Embedding: Link
tSNE Demo: Link
Swiss Roll: Link
PCA Proofs from Professor Jerry Zhu's 540 notes: PDF File
Google Robotics: Link
ChatGPT RL from human feedback: Link
AlphaGO: Link
Autonomous driving (may not work): Link
Q Learning: Link
Multi-Armed Bandit math: Link, Link
Deep reinforcement learning: Link
Learning in games: Link
How to do hierarchical clustering for 1D points? Link
How to do hierarchical clustering given pairwise distance table? Link
How to update cluster centers for K-means clustering? Link
How to find the cluster center so that a fixed number of items are assigned to each K-means cluster? Link
How to find the cluster center so that one of the clusters is empty? Link (Part 9)
How to compute projection? Link
How to compute new features based on PCA? Link
How to compute the projected variance? Link (Part 8)
How to compute optimal value function? Link
# Summary
📗 Tuesday to Friday lectures: 1:00 to 2:15, Zoom Link
📗 Monday to Saturday office hours: Zoom Link
📗 Personal meeting room: always open, Zoom Link
📗 Math Homework:
M7,
M8,
📗 Programming Homework:
P4,
📗 Examples and Quizzes:
Q15,
Q16,
📗 Discussions:
D7,
D8,
# Lectures
📗 Slides (will be posted before lecture, usually updated on Monday):
Blank Slides:
Part 1: PDF,
Part 2: PDF,
Part 3: PDF,
Part 4: PDF,
📗 The annotated lecture slides will not be posted this year: please copy down the notes during the lecture or from the Zoom recording.
📗 Notes

Image by bismart
# Other Materials
📗 Pre-recorded videos from 2020
Lecture 15 Part 1 (Unsupervised Learning): Link Lecture 15 Part 2 (Hierarchical Clustering): Link
Lecture 15 Part 3 (K Means Clustering): Link
Lecture 16 Part 1 (Dimensionality Reduction): Link
Lecture 16 Part 2 (Principal Component): Link
Lecture 16 Part 3 (Non-linear PCA): Link
📗 Relevant websites
Image Segmentation: Link 1, Link 2 Hierachical Clustering: Link
Tree of Life: Link 1, Link 2
K Means Clustering: Link
K Gaussian Mixture: Link
Word Embedding: Link
Principal Component: Link
Eigen Face: Link 1, Link 2
t-distributed Stochastic Neighbor Embedding: Link
tSNE Demo: Link
Swiss Roll: Link
PCA Proofs from Professor Jerry Zhu's 540 notes: PDF File
Google Robotics: Link
ChatGPT RL from human feedback: Link
AlphaGO: Link
Autonomous driving (may not work): Link
Q Learning: Link
Multi-Armed Bandit math: Link, Link
Deep reinforcement learning: Link
Learning in games: Link
📗 YouTube videos from previous summers
📗 Hierarchical Clustering
How to update distance table for hierarchical clustering? Link How to do hierarchical clustering for 1D points? Link
How to do hierarchical clustering given pairwise distance table? Link
📗 K-Means Clustering
What is the relationship between K Means and Gradient Descent? Link How to update cluster centers for K-means clustering? Link
How to find the cluster center so that a fixed number of items are assigned to each K-means cluster? Link
How to find the cluster center so that one of the clusters is empty? Link (Part 9)
📗 PCA
Why is PCA solving eigenvalues and eigenvectors? Part 1, Part 2, Part 3 How to compute projection? Link
How to compute new features based on PCA? Link
How to compute the projected variance? Link (Part 8)
📗 Reinforcement Learning
How to compute value function given policy? Link How to compute optimal value function? Link
# Keywords and Notations
📗 Clustering
📗 Single Linkage: \(d\left(C_{k}, C_{k'}\right) = \displaystyle\min\left\{d\left(x_{i}, x_{i'}\right) : x_{i} \in C_{k}, x_{i'} \in C_{k'}\right\}\), where \(C_{k}, C_{k'}\) are two clusters (set of points), \(d\) is the distance function.
📗 Complete Linkage: \(d\left(C_{k}, C_{k'}\right) = \displaystyle\max\left\{d\left(x_{i}, x_{i'}\right) : x_{i} \in C_{k}, x_{i'} \in C_{k'}\right\}\).
📗 Average Linkage: \(d\left(C_{k}, C_{k'}\right) = \dfrac{1}{\left| C_{k} \right| \left| C_{k'} \right|} \displaystyle\sum_{x_{i} \in C_{k}, x_{i'} \in C_{k'}} d\left(x_{i}, x_{i'}\right)\), where \(\left| C_{k} \right|, \left| C_{k'} \right|\) are the number of the points in the clusters.
📗 Distortion (Euclidean distance): \(D_{K} = \displaystyle\sum_{i=1}^{n} d\left(x_{i}, c_{k^\star\left(x_{i}\right)}\left(x_{i}\right)\right)^{2}\), \(k^\star\left(x\right) = \mathop{\mathrm{argmin}}_{k = 1, 2, ..., K} d\left(x, c_{k}\right)\), where \(k^\star\left(x\right)\) is the cluster \(x\) belongs to.
📗 K-Means Gradient Descent Step: \(c_{k} = \dfrac{1}{\left| C_{k} \right|} \displaystyle\sum_{x \in C_{k}} x\).
📗 Projection: \(\text{proj} _{u_{k}} x_{i} = \left(\dfrac{u_{k^\top} x_{i}}{u_{k^\top} u_{k}}\right) u_{k}\) with length \(\left\|\text{proj} _{u_{k}} x_{i}\right\|_{2} = \left(\dfrac{u_{k^\top} x_{i}}{u_{k^\top} u_{k}}\right)\), where \(u_{k}\) is a principal direction.
📗 Projected Variance (Scalar form, MLE): \(V = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \left(u_{k^\top} x_{i} - \mu_{k}\right)^{2}\) such that \(u_{k^\top} u_{k} = 1\), where \(\mu_{k} = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} u_{k^\top} x_{i}\).
📗 Projected Variance (Matrix form, MLE): \(V = u_{k^\top} \hat{\Sigma} u_{k}\) such that \(u_{k^\top} u_{k} = 1\), where \(\hat{\Sigma}\) is the convariance matrix of the data: \(\hat{\Sigma} = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \left(x_{i} - \hat{\mu}\right)\left(x_{i} - \hat{\mu}\right)^\top\), \(\hat{\mu} = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} x_{i}\).
📗 New Feature: \(\left(u_{1^\top} x_{i}, u_{2^\top} x_{i}, ..., u_{K^\top} x_{i}\right)^\top\).
📗 Reconstruction: \(x_{i} = \displaystyle\sum_{i=1}^{m} \left(u_{k^\top} x_{i}\right) u_{k} \approx \displaystyle\sum_{i=1}^{K} \left(u_{k^\top} x_{i}\right) u_{k}\) with \(u_{k^\top} u_{k} = 1\).
📗 Uninformed Search
📗 Breadth First Search (Time Complexity): \(T = 1 + b + b^{2} + ... + b^{d}\), where \(b\) is the branching factor (number of children per node) and \(d\) is the depth of the goal state.
📗 Breadth First Search (Space Complexity): \(S = b^{d}\).
📗 Depth First Search (Time Complexity): \(T = b^{D-d+1} + ... + b^{D-1} + b^{D}\), where \(D\) is the depth of the leafs.
📗 Depth First Search (Space Complexity): \(S = \left(b - 1\right) D + 1\).
📗 Iterative Deepening Search (Time Complexity): \(T = d + d b + \left(d - 1\right) b^{2} + ... + 3 b^{d-2} + 2 b^{d-1} + b^{d}\).
📗 Iterative Deepening Search (Space Complexity): \(S = \left(b - 1\right) d + 1\).
📗 Informed Search
📗 Admissible Heuristic: \(h : 0 \leq h\left(s\right) \leq h^\star\left(s\right)\), where \(h^\star\left(s\right)\) is the actual cost from state \(s\) to the goal state, and \(g\left(s\right)\) is the actual cost of the initial state to \(s\).
Last Updated: January 19, 2026 at 9:18 PM