Prev: W7 Next: W8
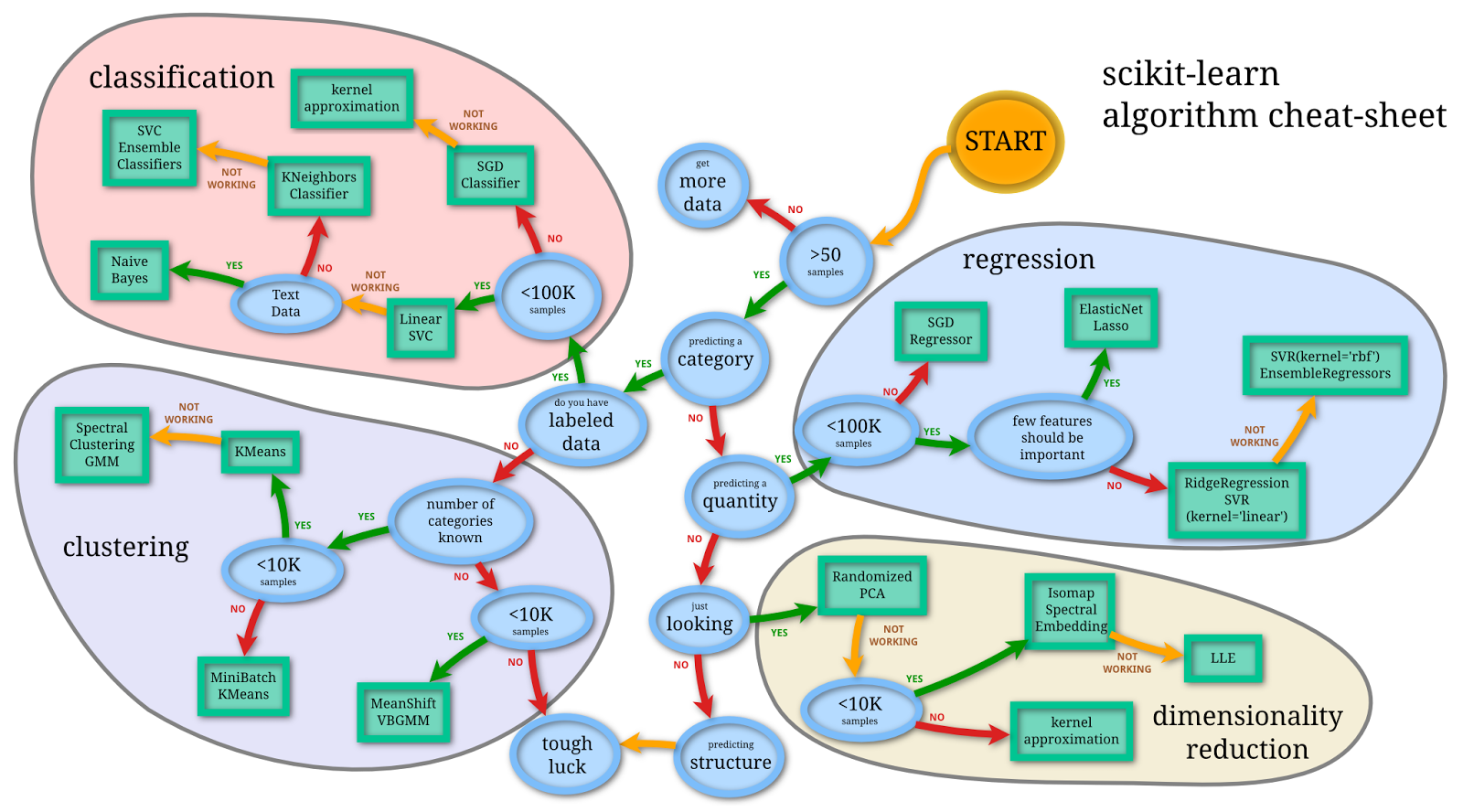
Image by scikit learn
W6 : M9 and M10
W7 : M11
Practice: X5 and X6 and X7 and X8
F2A Permutations: Link
F1B Permutations: Link
F2B Permutations: Link
F1A: Mean = 75.6%, Stdev = 16.14
F1B: Mean = 71.23%, Stdev = 14.57
F2A: Mean = 75.32%, Stdev = 21.89
F2B: Mean = 72.56%, Stdev = 23.9
(2) The slides subtitled "Motivation" and "Discussion" contain concepts you should be familiar with, but the specific mathematics will not be tested on the exam.
(3) The slides subtitled "Description" and "Algorithm" are mostly useful for programming homework, not exams.
(4) The slides subtitled "Admin" are not relevant to the course materials.
(2) Around a third of the questions will be similar to the homework or quiz or past exam questions (similar method to solve the problems).
(3) Around a third of the questions will be new, mostly from topics not covered in the homework, and reading the slides will be helpful.
Lecture 24 (Mechanism Design): Interactive Lecture (see Canvas Zoom recording)
EX2: Link
CX3: Link
CX4: Link
2023 Online Exams:
F1A: Link
F2A: Link
F1B: Link
F2B: Link
2022 Online Exams:
F1A-C: Link
F2A-C: Link
FB-C: Link
FA-E: Link
FB-E: Link
2021 Online Exams:
F1A-C: Link
F1B-C: Link
F2A-C: Link
F2B-C: Link
2020 Online Exams:
F1A-C: Link
F1B-C: Link
F2A-C: Link
F2B-C: Link
F1A-E: Link
F1B-E: Link
F2A-E: Link
F2B-E: Link
2019 In-person Exams:
Final Version A: File
Version A Answers: CECBC DBBBA BEEDD BCACB CBEED DDCDC ACBCC ECABC
Final Version B: File
Version B Answers: EEAEE AEACE BBDED BDAAA DCEEA CDACA AEAAA CCABB
Sample final: Link
How to do hierarchical clustering for 1D points? Link
How to do hierarchical clustering given pairwise distance table? Link
How to update cluster centers for K-means clustering? Link
How to find the cluster center so that a fixed number of items are assigned to each K-means cluster? Link
How to find the cluster center so that one of the clusters is empty? Link (Part 9)
How to compute projection? Link
How to compute new features based on PCA? Link
How to compute the projected variance? Link (Part 8)
How to compute optimal value function? Link
How to get expansion path for DFS? Link
How to get expansion path for IDS? Link
What is the shape of tree for IDS to search the quickest? Link
How to do backtracking for search problems? Link
How to compute time complexity for multi-branch trees? Link
How to find the best case time complexity? Link (Part 4)
What is the shape of the tree that minimizes the time complexity of IDS? Link (Part 8)
What is the minimum number of nodes searched given the goal depth? Link (Part 4)
How to find the number of states expanded during search for a large tree? Link (Part 12)
How to find all possible configurations of the 3-puzzle? Link (Part 1)
How to find the time complexity on binary search tree with large number of nodes? Link (Part 2, Part 3)
How to find the shape of a search tree such that IDS is the quickest? Link (Part 1)
How to get expansion path for BFGS? Link
How to get expansion path for A? Link
How to get expansion path for A*? Link
How to check if a heuristic is admissible? Link
How to find the expansion sequence for uniform cost search? Link
Which functions of two admissible heuristic are still admissible? Link
How to do A search on a maze? Link (Part 2)
How to do hill climbing for SAT problems? Link
What is the number of flips needed to move from one binary sequence to another? Link (Part 7)
What is the local minimum of a linear function with three variables? Link (Part 14)
How to use hill climbing to solve the graph coloring problem? Link (Part 7)
How to do hill climbing on 3D state spaces? Link (Part 1)
How to find the shortest sequence of flipping consecutive entries to reach a specific configuration? Link
Which temperature would minimize the probability of moving in simulated annealing? Link (Part 2)
How to find the state with the highest reproduction probability given the argmax-argmin fitness functions? Link (Part 1, Part 2)
How to compute reproduction probabilities? Link
How to solve the pirate game? Link
How to solve the wage competition game (sequential version)? Link
How to solve a simple game with Chance? Link
How to figure out which branches can be pruned using Alpha Beta algorithm? Simple Link, Complicated Link
How to solve the Rubinstein Bargaining problem? Link
How to figure out which nodes are alpha-beta pruned? Link
How to find the solution of the II-nim game? Link (Part 2)
How to find the solution of a game with Chance? Link (Part 11)
How to compute the value of a game with Chance? Link (Part 11)
How to reorder the branches so that alpha-beta pruning will prune the largest number of nodes? Link (Part 13)
What is the order of the branches that maximizes the number of alpha-beta pruned nodes? Link (Part 13)
How to reorder the subtrees so that alpha-beta would prune the largest number of nodes? Link (Part 1)
How to find the value of the game for II-nim games? Link (Part 2)
How to solve for the SPE for a game with Chance? Link (Part 3)
How to do iterated elimination of strictly dominated strategies (IESDS)? Link
How to find the mixed strategy Nash equilibrium of a simple 2 by 2 game? Link
What is the median voter theorem? Link
How to guess and check a mixed strategy Nash equilibrium of a simple 3 by 3 game? Link
How to solve the mixing probabilities of the volunteer's dilemma game? Link
What is the Nash equilibrium of the vaccination game? Link
How to find the mixed strategy best responses? Link
How to compute the Nash equilibrium for zero-sum matrix games? Link
How to draw the best responses functions with mixed strategies? Link
How to compute the pure Nash equilibrium of the high way game? Link (Part 5)
What is the value of a mixed strategy Nash equilibrium? Link (Part 6)
How to compute the pure Nash equilibrium of the vaccination game? Link (Part 5)
How to find the value of the battle of the sexes game? Link (Part 6)
How to redesign the game to implement a Nash equilibrium? Link (Part 10)
How to find all Nash equilibria using best response functions? Link (Part 1)
How to compute the Nash equilibrium of the pollution game? Link (Part 3)
How to compute a symmetric mixed strategy Nash equilibrium for the volunteer's dilemma game? Link (Part 10)
How to perform iterated elimination of strictly dominated strategies? Link (Part 14)
How to compute the Nash equilibrium where only one player mixes? Link (Part 1)
How to compute the mixed Nash for the battle of sexes game? Link (Part 1)
How to compute the game with indifferences where only one player mixes? Link (Part 2)
How to modify the game so that a specific entry is the Nash? Link (Part 1)
What is the Nash equilibrium of a the highway game? Link (Part 2)
What is the Nash equilibrium of the pollution game? Link (Part 3)
How to find the Nash equilibrium of the vaccination game? Link (Part 4)
# Summary
📗 Tuesday to Friday lectures: 1:00 to 2:15, Zoom Link
📗 Monday to Saturday office hours: Zoom Link
📗 Personal meeting room: always open, Zoom Link
📗 Math Homework:
M7,
M8,
M9,
M10,
M11,
📗 Programming Homework:
P4,
P5,
📗 Examples and Quizzes:
Q15,
Q16,
Q17,
Q18,
Q19,
Q20,
Q20,
Q22,
Q23,
Q24,
📗 Discussions:
D7,
D8,
D9,
D10,
D11,
D12,
# Lectures
📗 Slides (will be posted before lecture, usually updated on Monday):
Blank Slides:
Part 1: PDF,
Part 2: PDF,
📗 The annotated lecture slides will not be posted this year: please copy down the notes during the lecture or from the Zoom recording.
📗 Notes

Image by scikit learn
# Summary
📗 Coverage: unsupervised learning + reinforcement learning + search + game theory W5 to W7.
📗 Number of questions: 30
📗 Length: 2 x 1 hour 15 minutes
📗 Regular: August 10 AMD August 11, 1:00 to 2:30 PM
📗 Make-up: August 10 AND August 11, 9:00 to 10:30 PM
📗 Link to relevant pages:
W5 : M7 and M8 W6 : M9 and M10
W7 : M11
Practice: X5 and X6 and X7 and X8
# Exams
F1A Permutations: LinkF2A Permutations: Link
F1B Permutations: Link
F2B Permutations: Link
F1A: Mean = 75.6%, Stdev = 16.14
| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| MAX | 3 | 3 | 3 | 3 | 2 | 3 | 4 | 2 | 4 | 3 | 3 | 4 | 3 | 4 | 1 |
| PROB | 1 | 0.94 | 0.67 | 0.91 | 0.93 | 0.96 | 0.52 | 0.93 | 0.20 | 0.83 | 0.81 | 0.67 | 0.98 | 0.81 | 1 |
| RPBI | 0 | 4.48 | 7.01 | 5.87 | 3.43 | 4.06 | 7.71 | 3.61 | 2.44 | 6.93 | 7.01 | 9.35 | 2.95 | 7.92 | 0 |
F1B: Mean = 71.23%, Stdev = 14.57
| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| MAX | 4 | 3 | 4 | 3 | 2 | 3 | 4 | 4 | 3 | 3 | 4 | 4 | 4 | 5.79 | 1 |
| PROB | 0.09 | 0.77 | 0.42 | 0.46 | 0.91 | 0.84 | 0.67 | 0.88 | 0.88 | 0.84 | 0.77 | 1 | 0.75 | 1 | 1 |
| RPBI | 0.80 | 7.38 | 6.25 | 3.78 | 4.14 | 7.28 | 9.42 | 8.68 | 6.93 | 6.87 | 10.39 | 0 | 10.42 | 0 | 0 |
F2A: Mean = 75.32%, Stdev = 21.89
| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| MAX | 3 | 3 | 3 | 3 | 2 | 3 | 4 | 4 | 4 | 4 | 3 | 4 | 3 | 4 | 1 |
| PROB | 1 | 0.89 | 0.50 | 0.83 | 0.89 | 0.83 | 0.72 | 0.56 | 0.11 | 0.89 | 0.61 | 0.44 | 0.89 | 0.72 | 1 |
| RPBI | 0 | 1.57 | 1.43 | 1.58 | 1.07 | 1.78 | 2.47 | 2.11 | 0.27 | 2.14 | 1.66 | 1.69 | 1.60 | 2.09 | 0 |
F2B: Mean = 72.56%, Stdev = 23.9
| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| MAX | 3 | 3 | 4 | 3 | 2 | 3 | 4 | 4 | 4 | 3 | 4 | 3 | 3 | 5.79 | 1 |
| PROB | 0.13 | 0.67 | 0.47 | 0.40 | 0.80 | 0.60 | 0.20 | 0.67 | 0.80 | 0.80 | 0.67 | 1 | 0.67 | 1 | 1 |
| RPBI | 0.20 | 1.42 | 1.30 | 0.88 | 0.96 | 1.32 | 0.48 | 1.61 | 1.92 | 1.28 | 1.89 | 0 | 1.42 | 0 | 0 |
# Details
📗 Slides:
(1) The slides subtitled "Definition" and "Quiz" contain the mathematics and statistics that you are required to know for the exams. (2) The slides subtitled "Motivation" and "Discussion" contain concepts you should be familiar with, but the specific mathematics will not be tested on the exam.
(3) The slides subtitled "Description" and "Algorithm" are mostly useful for programming homework, not exams.
(4) The slides subtitled "Admin" are not relevant to the course materials.
📗 Questions:
(1) Around a third of the questions will be identical to the homework or quiz or past exam questions (different randomization of parameters), you can practice by solving these question again with someone else's ID (auto-grading will not work if you do not enter an ID). (2) Around a third of the questions will be similar to the homework or quiz or past exam questions (similar method to solve the problems).
(3) Around a third of the questions will be new, mostly from topics not covered in the homework, and reading the slides will be helpful.
📗 Question types:
All questions will ask you to enter a number, vector (or list of options), or matrix. There will be no drawing or selecting objects on a canvas, and no text entry or essay questions. You will not get the hints like the ones in the homework. You can type your answers in a text file directly and submit it on Canvas. If you use the website, you can use the "calculate" button to make sure the expression you entered can be evaluated correctly when graded. You will receive 0 for incorrect answers and not-evaluate-able expressions, no partial marks, and no additional penalty for incorrect answers. # Other Materials
📗 Pre-recorded videos from 2020
Lecture 23 (Repeated Games): Interactive Lecture (see Canvas Zoom recording) Lecture 24 (Mechanism Design): Interactive Lecture (see Canvas Zoom recording)
📗 Relevant websites
2024 Online and In-Person Exams: EX2: Link
CX3: Link
CX4: Link
2023 Online Exams:
F1A: Link
F2A: Link
F1B: Link
F2B: Link
2022 Online Exams:
F1A-C: Link
F2A-C: Link
FB-C: Link
FA-E: Link
FB-E: Link
2021 Online Exams:
F1A-C: Link
F1B-C: Link
F2A-C: Link
F2B-C: Link
2020 Online Exams:
F1A-C: Link
F1B-C: Link
F2A-C: Link
F2B-C: Link
F1A-E: Link
F1B-E: Link
F2A-E: Link
F2B-E: Link
2019 In-person Exams:
Final Version A: File
Version A Answers: CECBC DBBBA BEEDD BCACB CBEED DDCDC ACBCC ECABC
Final Version B: File
Version B Answers: EEAEE AEACE BBDED BDAAA DCEEA CDACA AEAAA CCABB
Sample final: Link
📗 YouTube videos from previous summers
📗 Hierarchical Clustering
How to update distance table for hierarchical clustering? Link How to do hierarchical clustering for 1D points? Link
How to do hierarchical clustering given pairwise distance table? Link
📗 K-Means Clustering
What is the relationship between K Means and Gradient Descent? Link How to update cluster centers for K-means clustering? Link
How to find the cluster center so that a fixed number of items are assigned to each K-means cluster? Link
How to find the cluster center so that one of the clusters is empty? Link (Part 9)
📗 PCA
Why is PCA solving eigenvalues and eigenvectors? Part 1, Part 2, Part 3 How to compute projection? Link
How to compute new features based on PCA? Link
How to compute the projected variance? Link (Part 8)
📗 Reinforcement Learning
How to compute value function given policy? Link How to compute optimal value function? Link
📗 Uninformed Search
How to get expansion path for BFS? Link How to get expansion path for DFS? Link
How to get expansion path for IDS? Link
What is the shape of tree for IDS to search the quickest? Link
How to do backtracking for search problems? Link
How to compute time complexity for multi-branch trees? Link
How to find the best case time complexity? Link (Part 4)
What is the shape of the tree that minimizes the time complexity of IDS? Link (Part 8)
What is the minimum number of nodes searched given the goal depth? Link (Part 4)
How to find the number of states expanded during search for a large tree? Link (Part 12)
How to find all possible configurations of the 3-puzzle? Link (Part 1)
How to find the time complexity on binary search tree with large number of nodes? Link (Part 2, Part 3)
How to find the shape of a search tree such that IDS is the quickest? Link (Part 1)
📗 Informed Search
How to get expansion path for UCS? Link How to get expansion path for BFGS? Link
How to get expansion path for A? Link
How to get expansion path for A*? Link
How to check if a heuristic is admissible? Link
How to find the expansion sequence for uniform cost search? Link
Which functions of two admissible heuristic are still admissible? Link
How to do A search on a maze? Link (Part 2)
📗 Hill Climbing
How to do hill climbing on 2D state spaces? Link How to do hill climbing for SAT problems? Link
What is the number of flips needed to move from one binary sequence to another? Link (Part 7)
What is the local minimum of a linear function with three variables? Link (Part 14)
How to use hill climbing to solve the graph coloring problem? Link (Part 7)
How to do hill climbing on 3D state spaces? Link (Part 1)
How to find the shortest sequence of flipping consecutive entries to reach a specific configuration? Link
📗 Simulated Annealing
How to find the probability of moving in simulated annealing? Link Which temperature would minimize the probability of moving in simulated annealing? Link (Part 2)
📗 Genetic Algorithm
How to find reproduction probabilities? Link How to find the state with the highest reproduction probability given the argmax-argmin fitness functions? Link (Part 1, Part 2)
How to compute reproduction probabilities? Link
📗 Extensive Form Game
How to solve the lions game? Link How to solve the pirate game? Link
How to solve the wage competition game (sequential version)? Link
How to solve a simple game with Chance? Link
How to figure out which branches can be pruned using Alpha Beta algorithm? Simple Link, Complicated Link
How to solve the Rubinstein Bargaining problem? Link
How to figure out which nodes are alpha-beta pruned? Link
How to find the solution of the II-nim game? Link (Part 2)
How to find the solution of a game with Chance? Link (Part 11)
How to compute the value of a game with Chance? Link (Part 11)
How to reorder the branches so that alpha-beta pruning will prune the largest number of nodes? Link (Part 13)
What is the order of the branches that maximizes the number of alpha-beta pruned nodes? Link (Part 13)
How to reorder the subtrees so that alpha-beta would prune the largest number of nodes? Link (Part 1)
How to find the value of the game for II-nim games? Link (Part 2)
How to solve for the SPE for a game with Chance? Link (Part 3)
📗 Normal Form Game
How to find the Nash equilibrium of a zero sum game? Link How to do iterated elimination of strictly dominated strategies (IESDS)? Link
How to find the mixed strategy Nash equilibrium of a simple 2 by 2 game? Link
What is the median voter theorem? Link
How to guess and check a mixed strategy Nash equilibrium of a simple 3 by 3 game? Link
How to solve the mixing probabilities of the volunteer's dilemma game? Link
What is the Nash equilibrium of the vaccination game? Link
How to find the mixed strategy best responses? Link
How to compute the Nash equilibrium for zero-sum matrix games? Link
How to draw the best responses functions with mixed strategies? Link
How to compute the pure Nash equilibrium of the high way game? Link (Part 5)
What is the value of a mixed strategy Nash equilibrium? Link (Part 6)
How to compute the pure Nash equilibrium of the vaccination game? Link (Part 5)
How to find the value of the battle of the sexes game? Link (Part 6)
How to redesign the game to implement a Nash equilibrium? Link (Part 10)
How to find all Nash equilibria using best response functions? Link (Part 1)
How to compute the Nash equilibrium of the pollution game? Link (Part 3)
How to compute a symmetric mixed strategy Nash equilibrium for the volunteer's dilemma game? Link (Part 10)
How to perform iterated elimination of strictly dominated strategies? Link (Part 14)
How to compute the Nash equilibrium where only one player mixes? Link (Part 1)
How to compute the mixed Nash for the battle of sexes game? Link (Part 1)
How to compute the game with indifferences where only one player mixes? Link (Part 2)
How to modify the game so that a specific entry is the Nash? Link (Part 1)
What is the Nash equilibrium of a the highway game? Link (Part 2)
What is the Nash equilibrium of the pollution game? Link (Part 3)
How to find the Nash equilibrium of the vaccination game? Link (Part 4)
# Keywords and Notations
📗 Clustering
📗 Single Linkage: \(d\left(C_{k}, C_{k'}\right) = \displaystyle\min\left\{d\left(x_{i}, x_{i'}\right) : x_{i} \in C_{k}, x_{i'} \in C_{k'}\right\}\), where \(C_{k}, C_{k'}\) are two clusters (set of points), \(d\) is the distance function.
📗 Complete Linkage: \(d\left(C_{k}, C_{k'}\right) = \displaystyle\max\left\{d\left(x_{i}, x_{i'}\right) : x_{i} \in C_{k}, x_{i'} \in C_{k'}\right\}\).
📗 Average Linkage: \(d\left(C_{k}, C_{k'}\right) = \dfrac{1}{\left| C_{k} \right| \left| C_{k'} \right|} \displaystyle\sum_{x_{i} \in C_{k}, x_{i'} \in C_{k'}} d\left(x_{i}, x_{i'}\right)\), where \(\left| C_{k} \right|, \left| C_{k'} \right|\) are the number of the points in the clusters.
📗 Distortion (Euclidean distance): \(D_{K} = \displaystyle\sum_{i=1}^{n} d\left(x_{i}, c_{k^\star\left(x_{i}\right)}\left(x_{i}\right)\right)^{2}\), \(k^\star\left(x\right) = \mathop{\mathrm{argmin}}_{k = 1, 2, ..., K} d\left(x, c_{k}\right)\), where \(k^\star\left(x\right)\) is the cluster \(x\) belongs to.
📗 K-Means Gradient Descent Step: \(c_{k} = \dfrac{1}{\left| C_{k} \right|} \displaystyle\sum_{x \in C_{k}} x\).
📗 Projection: \(\text{proj} _{u_{k}} x_{i} = \left(\dfrac{u_{k^\top} x_{i}}{u_{k^\top} u_{k}}\right) u_{k}\) with length \(\left\|\text{proj} _{u_{k}} x_{i}\right\|_{2} = \left(\dfrac{u_{k^\top} x_{i}}{u_{k^\top} u_{k}}\right)\), where \(u_{k}\) is a principal direction.
📗 Projected Variance (Scalar form, MLE): \(V = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \left(u_{k^\top} x_{i} - \mu_{k}\right)^{2}\) such that \(u_{k^\top} u_{k} = 1\), where \(\mu_{k} = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} u_{k^\top} x_{i}\).
📗 Projected Variance (Matrix form, MLE): \(V = u_{k^\top} \hat{\Sigma} u_{k}\) such that \(u_{k^\top} u_{k} = 1\), where \(\hat{\Sigma}\) is the convariance matrix of the data: \(\hat{\Sigma} = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \left(x_{i} - \hat{\mu}\right)\left(x_{i} - \hat{\mu}\right)^\top\), \(\hat{\mu} = \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} x_{i}\).
📗 New Feature: \(\left(u_{1^\top} x_{i}, u_{2^\top} x_{i}, ..., u_{K^\top} x_{i}\right)^\top\).
📗 Reconstruction: \(x_{i} = \displaystyle\sum_{i=1}^{m} \left(u_{k^\top} x_{i}\right) u_{k} \approx \displaystyle\sum_{i=1}^{K} \left(u_{k^\top} x_{i}\right) u_{k}\) with \(u_{k^\top} u_{k} = 1\).
📗 Uninformed Search
📗 Breadth First Search (Time Complexity): \(T = 1 + b + b^{2} + ... + b^{d}\), where \(b\) is the branching factor (number of children per node) and \(d\) is the depth of the goal state.
📗 Breadth First Search (Space Complexity): \(S = b^{d}\).
📗 Depth First Search (Time Complexity): \(T = b^{D-d+1} + ... + b^{D-1} + b^{D}\), where \(D\) is the depth of the leafs.
📗 Depth First Search (Space Complexity): \(S = \left(b - 1\right) D + 1\).
📗 Iterative Deepening Search (Time Complexity): \(T = d + d b + \left(d - 1\right) b^{2} + ... + 3 b^{d-2} + 2 b^{d-1} + b^{d}\).
📗 Iterative Deepening Search (Space Complexity): \(S = \left(b - 1\right) d + 1\).
📗 Informed Search
📗 Admissible Heuristic: \(h : 0 \leq h\left(s\right) \leq h^\star\left(s\right)\), where \(h^\star\left(s\right)\) is the actual cost from state \(s\) to the goal state, and \(g\left(s\right)\) is the actual cost of the initial state to \(s\).
📗 Local Search
📗 Hill Climbing (Valley Finding), probability of moving from \(s\) to a state \(s'\) \(p = 0\) if \(f\left(s'\right) \geq f\left(s\right)\) and \(p = 1\) if \(f\left(s'\right) < f\left(s\right)\), where \(f\left(s\right)\) is the cost of the state \(s\).
📗 Simulated Annealing, probability of moving from \(s\) to a worse state \(s'\) = \(p = e^{- \dfrac{\left| f\left(s'\right) - f\left(s\right) \right|}{T\left(t\right)}}\) if \(f\left(s'\right) \geq f\left(s\right)\) and \(p = 1\) if \(f\left(s'\right) < f\left(s\right)\), where \(T\left(t\right)\) is the temperature as time \(t\).
📗 Genetic Algorithm, probability of get selected as a parent in cross-over: \(p_{i} = \dfrac{F\left(s_{i}\right)}{\displaystyle\sum_{j=1}^{n} F\left(s_{j}\right)}\), \(i = 1, 2, ..., N\), where \(F\left(s\right)\) is the fitness of state \(s\).
📗 Adversarial Search
📗 Sequential Game (Alpha Beta Pruning): prune the tree if \(\alpha \geq \beta\), where \(\alpha\) is the current value of the MAX player and \(\beta\) is the current value of the MIN player.
📗 Simultaneous Move Game (rationalizable): remove an action \(s_{i}\) of player \(i\) if it is strictly dominated \(F\left(s_{i}, s_{-i}\right) < F\left(s'_{i}, s_{-i}\right)\), for some \(s'_{i}\) of player \(i\) and for all \(s_{-i}\) of the other players.
📗 Simultaneous Move Game (Nash equilibrium): \(\left(s_{i}, s_{-i}\right)\) is a (pure strategy) Nash equilibrium if \(F\left(s_{i}, s_{-i}\right) \geq F\left(s'_{i}, s_{-i}\right)\) and \(F\left(s_{i}, s_{-i}\right) \geq F\left(s_{i}, s'_{-i}\right)\), for all \(s'_{i}, s'_{-i}\).
Last Updated: January 19, 2026 at 9:18 PM