Prev: W3 Next: W5
Blank Slides (with blank pages for quiz questions): Part 1, Part 2,
Annotated Slides: Part 1, Part 2,
Saturday: PDF.
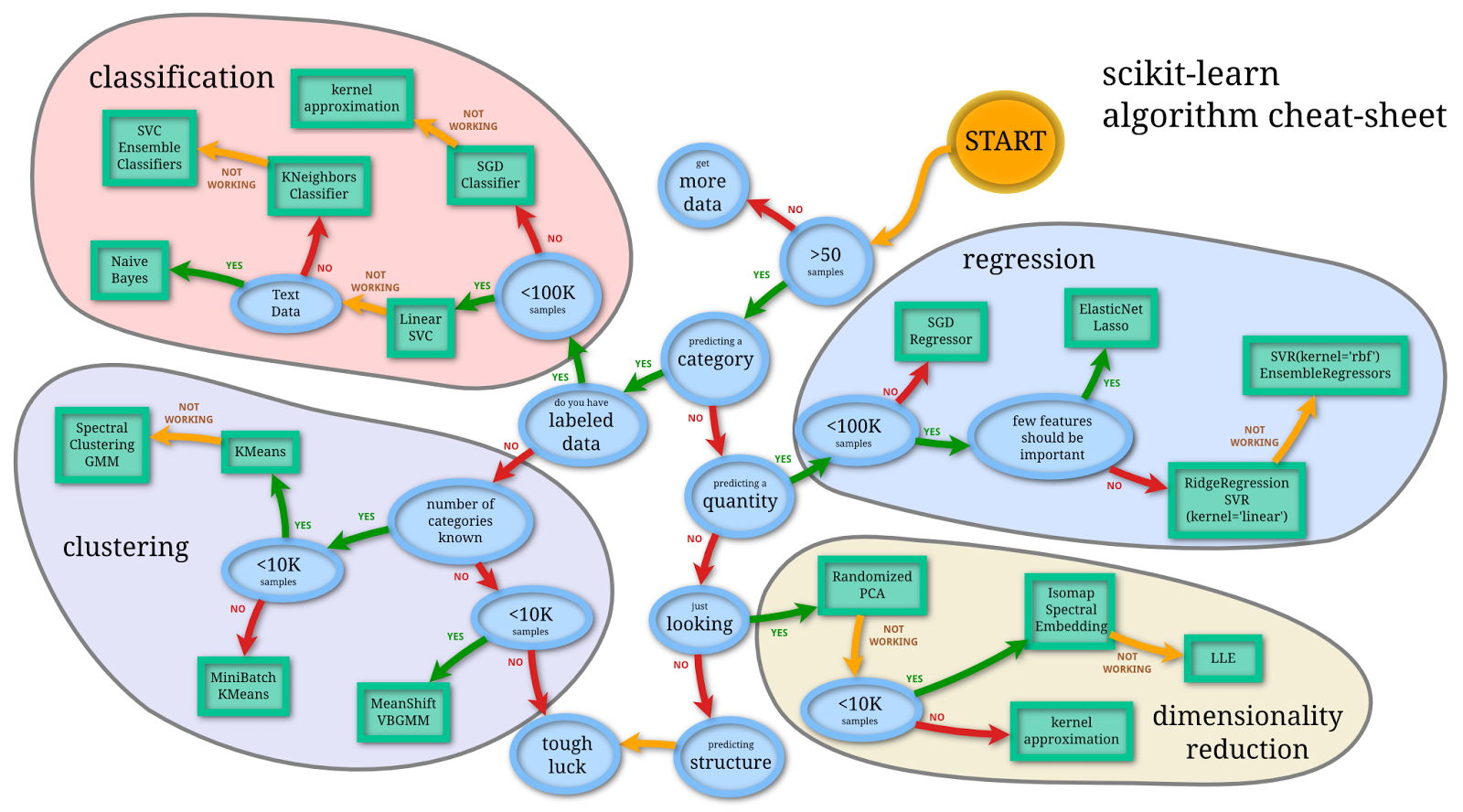
Image by scikit learn
Exam M2A: Mean = 74.43%, Stdev = 21.66
Exam MB: Mean = 65.07%, Stdev = 29.1
PROB is the percentage of students who get this question correct.
RPBI is the (point biserial) correlation between getting this question correct with the total grade on the exam.
PROB < 0.25 or RPBI < 0 means this question is probably not well-made.
W2 : M4 and M5
W3 : M6 and M7
Practice: X1 and X2 and X3 and X6
(2) The slides subtitled "Motivation" and "Discussion" contain concepts you should be familiar with, but the specific mathematics will not be tested on the exam.
(3) The slides subtitled "Description" and "Algorithm" are mostly useful for programming homework, not exams.
(4) The slides subtitled "Admin" are not relevant to the course materials.
(2) Around a third of the questions will be similar to the past exam or quiz questions (ones that are covered during the lectures), going over the quiz questions will help, and solving the past exam questions will help.
(3) Around a third of the questions will be new, mostly from topics not covered in the homework, reading the slides will be helpful.
X1Q4-8 (SVMs): Link
X1Q9-10 (Kernels): Link
X1Q11-15 (KNN): Link
X2Q1-3 (Entropy): Link
X2Q4-6 (Decision Trees): Link
X2Q7-8 (Convolutions): Link
X2Q9-11 (CNNs): Link
X2Q12-15 (Probability): Link
X3Q1-3 (CPTs): Link
X3Q4-8 (Bayesian Networks): Link
Lecture 14 (Optimization): Guest Lecture (see Canvas Zoom recording)
EX1: Link
CX1: Link
CX2: Link
2023 Online Exams:
M1A: Link
M2A: Link
M1B: Link
M2B: Link
2022 Online Exams:
M1A-C: Link
M2A-C: Link
MB-C: Link
MA-E: Link
MB-E: Link
2021 Online Exams:
M1A-C: Link
M1B-C: Link
M2A-C: Link
M2B-C: Link
2020 Online Exams:
M1A-C: Link
M1B-C: Link
M2A-C: Link
M2B-C: Link
M1A-E: Link
M1B-E: Link
M2A-E: Link
M2B-E: Link
2019 In-person Exams:
Midterm Version A: Link
Version A Answers: ABEDE ECDDC CCBCC CEDBB CEECD DDDBC DBBAA AAADC
Midterm Version B: Link
Version B Answers: CCABD DAECE BCADC CCEBA DDCCD DDCCA AADBC ABDAB
Sample midterm: Link
M3Q6: Link
M4Q3: Link
M4Q6: Link
M4Q8: Link
M5Q8: Link
M6Q1: Link
M6Q4: Link
M7Q1: Link
M7Q4: Link
HMM: Link
Other Midterm Questions
Q2 (KNN Decision Boundary Question): Link
Q3 (KNN Leave-One-Out Question): Link
Q4 (CNN Count Weights Question): Link
Q5 (Naive Bayes Count CPTs Question): Link
Q7 (Please do NOT forget to submit your homework on Canvas! Question): Link
Test item: \(\left(x', y'\right)\), where \(j \in \left\{1, 2, ..., m\right\}\) is the feature index.
Perceptron algorithm update step: \(w = w - \alpha \left(a_{i} - y_{i}\right) x_{i}\), \(b = b - \alpha \left(a_{i} - y_{i}\right)\), \(a_{i} = 1_{\left\{w^\top x_{i} + b \geq 0\right\}}\), where \(a_{i}\) is the activation value of instance \(i\).
Squared loss minimization of perceptrons: \(\left(\hat{w}, \hat{b}\right) = \mathop{\mathrm{argmin}}_{w, b} \dfrac{1}{2} \displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)^{2}\), \(a_{i} = g\left(w^\top x_{i} + b\right)\), where \(\hat{w}\) is the optimal weights, \(\hat{b}\) is the optimal bias, \(g\) is the activation function.
Loss minimization problem: \(\left(\hat{w}, \hat{b}\right) = \mathop{\mathrm{argmin}}_{w, b} -\displaystyle\sum_{i=1}^{n} \left(y_{i} \log\left(a_{i}\right) + \left(1 - y_{i}\right) \log\left(1 - a_{i}\right)\right)\), \(a_{i} = \dfrac{1}{1 + \exp\left(- \left(w^\top x_{i} + b\right)\right)}\).
Batch gradient descrent step: \(w = w - \alpha \displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right) x_{i}\), \(b = b - \alpha \displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)\), \(a_{i} = \dfrac{1}{1 + \exp\left(- \left(w^\top x_{i} + b\right)\right)}\), where \(\alpha\) is the learning rate.
\(a^{\left(1\right)}_{ij} = \dfrac{1}{1 + \exp\left(- \left(\left(\displaystyle\sum_{j'=1}^{m} x_{ij'} w^{\left(1\right)}_{j'j}\right) + b^{\left(1\right)}_{j}\right)\right)}\), where \(m\) is the number of features (or input units), \(w^{\left(1\right)}_{j' j}\) is the layer \(1\) weight from input unit \(j'\) to hidden layer unit \(j\), \(b^{\left(1\right)}_{j}\) is the bias for hidden layer unit \(j\), \(a_{ij}^{\left(1\right)}\) is the layer \(1\) activation of instance \(i\) hidden unit \(j\).
\(a^{\left(2\right)}_{i} = \dfrac{1}{1 + \exp\left(- \left(\left(\displaystyle\sum_{j=1}^{h} a^{\left(1\right)}_{ij} w^{\left(2\right)}_{j}\right) + b^{\left(2\right)}\right)\right)}\), where \(h\) is the number of hidden units, \(w^{\left(2\right)}_{j}\) is the layer \(2\) weight from hidden layer unit \(j\), \(b^{\left(2\right)}\) is the bias for the output unit, \(a^{\left(2\right)}_{i}\) is the layer \(2\) activation of instance \(i\).
Stochastic gradient descent step for two layer network with squared loss and logistic activation:
\(w^{\left(1\right)}_{j' j} = w^{\left(1\right)}_{j' j} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right) w_{j}^{\left(2\right)} a_{ij}^{\left(1\right)} \left(1 - a_{ij}^{\left(1\right)}\right) x_{ij'}\).
\(b^{\left(1\right)}_{j} \leftarrow b^{\left(1\right)}_{j} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right) w_{j}^{\left(2\right)} a_{ij}^{\left(1\right)} \left(1 - a_{ij}^{\left(1\right)}\right)\).
\(w^{\left(2\right)}_{j} \leftarrow w^{\left(2\right)}_{j} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right) a_{ij}^{\left(1\right)}\).
\(b^{\left(2\right)} \leftarrow b^{\left(2\right)} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right)\).
L2 regularization (sqaured loss): \(\displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)^{2} + \lambda \left(\displaystyle\sum_{j=1}^{m} \left(w_{j}\right)^{2} + b^{2}\right)\).
Hard margin, original max-margin formulation: \(\displaystyle\max_{w} \dfrac{2}{\sqrt{w^\top w}}\) such that \(w^\top x_{i} + b \leq -1\) if \(y_{i} = 0\) and \(w^\top x_{i} + b \geq 1\) if \(y_{i} = 1\).
Hard margin, simplified formulation: \(\displaystyle\min_{w} \dfrac{1}{2} w^\top w\) such that \(\left(2 y_{i} - 1\right)\left(w^\top x_{i} + b\right) \geq 1\).
Soft margin, original max-margin formulation: \(\displaystyle\min_{w} \dfrac{1}{2} w^\top w + \dfrac{1}{\lambda} \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \xi_{i}\) such that \(\left(2 y_{i} - 1\right)\left(w^\top x_{i} + b\right) \geq 1 - \xi, \xi \geq 0\), where \(\xi_{i}\) is the slack variable for instance \(i\), \(\lambda\) is the regularization parameter.
Soft margin, simplified formulation: \(\displaystyle\min_{w} \dfrac{\lambda}{2} w^\top w + \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \displaystyle\max\left\{0, 1 - \left(2 y_{i} - 1\right) \left(w^\top x_{i} + b\right)\right\}\)
Subgradient descent formula: \(w = \left(1 - \lambda\right) w - \alpha \left(2 y_{i} - 1\right) 1_{\left\{\left(2 y_{i} - 1\right) \left(w^\top x_{i} + b\right) \geq 1\right\}} x_{i}\).
Kernal Gram matrix: \(K_{i i'} = \varphi\left(x_{i}\right)^\top \varphi\left(x_{i'}\right)\).
Quadratic Kernel: \(K_{i i'} = \left(x_{i^\top} x_{i'} + 1\right)^{2}\) has feature representation \(\varphi\left(x_{i}\right) = \left(x_{i1}^{2}, x_{i2}^{2}, \sqrt{2} x_{i1} x_{i2}, \sqrt{2} x_{i1}, \sqrt{2} x_{i2}, 1\right)\).
Gaussian RBF Kernel: \(K_{i i'} = \exp\left(- \dfrac{1}{2 \sigma^{2}} \left(x_{i} - x_{i'}\right)^\top \left(x_{i} - x_{i'}\right)\right)\) has infinite-dimensional feature representation, where \(\sigma^{2}\) is the variance parameter.
Conditional entropy: \(H\left(Y | X\right) = -\displaystyle\sum_{x=1}^{K_{X}} p_{x} \displaystyle\sum_{y=1}^{K} p_{y|x} \log_{2} \left(p_{y|x}\right)\), where \(K_{X}\) is the number of possible values of feature, \(p_{x}\) is the fraction of data points with feature \(x\), \(p_{y|x}\) is the fraction of data points with label \(y\) among the ones with feature \(x\).
Information gain, for feature \(j\): \(I\left(Y | X_{j}\right) = H\left(Y\right) - H\left(Y | X_{j}\right)\).
Feature selection: \(j^\star = \mathop{\mathrm{argmax}}_{j} I\left(Y | X_{j}\right)\).
K-Nearest Neighbor classifier: \(\hat{y}_{i}\) = mode \(\left\{y_{\left(1\right)}, y_{\left(2\right)}, ..., y_{\left(k\right)}\right\}\), where mode is the majority label and \(y_{\left(t\right)}\) is the label of the \(t\)-th closest instance to instance \(i\) from the training set.
Maximum likelihood estimator (unigram): \(\hat{\mathbb{P}}\left\{z_{t}\right\} = \dfrac{c_{z_{t}}}{\displaystyle\sum_{z=1}^{m} c_{z}}\), where \(c_{z}\) is the number of time the token \(z\) appears in the training set and \(m\) is the vocabulary size (number of unique tokens).
Maximum likelihood estimator (unigram, with Laplace smoothing): \(\hat{\mathbb{P}}\left\{z_{t}\right\} = \dfrac{c_{z_{t}} + 1}{\left(\displaystyle\sum_{z=1}^{m} c_{z}\right) + m}\).
Bigram model: \(\mathbb{P}\left\{z_{1}, z_{2}, ..., z_{d}\right\} = \mathbb{P}\left\{z_{1}\right\} \displaystyle\prod_{t=2}^{d} \mathbb{P}\left\{z_{t} | z_{t-1}\right\}\).
Maximum likelihood estimator (bigram): \(\hat{\mathbb{P}}\left\{z_{t} | z_{t-1}\right\} = \dfrac{c_{z_{t-1}, z_{t}}}{c_{z_{t-1}}}\).
Maximum likelihood estimator (bigram, with Laplace smoothing): \(\hat{\mathbb{P}}\left\{z_{t} | z_{t-1}\right\} = \dfrac{c_{z_{t-1}, z_{t}} + 1}{c_{z_{t-1}} + m}\).
Joint probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y \in Y} \mathbb{P}\left\{X = x, Y = y\right\}\).
Bayes rule: \(\mathbb{P}\left\{Y = y | X = x\right\} = \dfrac{\mathbb{P}\left\{X = x | Y = y\right\} \mathbb{P}\left\{Y = y\right\}}{\displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}}\).
Law of total probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}\).
Independence: \(X, Y\) are independent if \(\mathbb{P}\left\{X = x, Y = y\right\} = \mathbb{P}\left\{X = x\right\} \mathbb{P}\left\{Y = y\right\}\) for every \(x, y\).
Conditional independence: \(X, Y\) are conditionally independent conditioned on \(Z\) if \(\mathbb{P}\left\{X = x, Y = y | Z = z\right\} = \mathbb{P}\left\{X = x | Z = z\right\} \mathbb{P}\left\{Y = y | Z = z\right\}\) for every \(x, y, z\).
Conditional Probability Table estimation (with Laplace smoothing): \(\hat{\mathbb{P}}\left\{x_{j} | p\left(X_{j}\right)\right\} = \dfrac{c_{x_{j}, p\left(X_{j}\right)} + 1}{c_{p\left(X_{j}\right)} + \left| X_{j} \right|}\), where \(\left| X_{j} \right|\) is the number of possible values of \(X_{j}\).
Bayesian network inference: \(\mathbb{P}\left\{x_{1}, x_{2}, ..., x_{m}\right\} = \displaystyle\prod_{j=1}^{m} \mathbb{P}\left\{x_{j} | p\left(X_{j}\right)\right\}\).
Naive Bayes estimation: .
Naive Bayes classifier: \(\hat{y}_{i} = \mathop{\mathrm{argmax}}_{y} \mathbb{P}\left\{Y = y | X = X_{i}\right\}\).
Convolution (2D): \(A = X \star W\), \(A_{j j'} = \displaystyle\sum_{s=-k}^{k} \displaystyle\sum_{t=-k}^{k} W_{s,t} X_{j-s,j'-t}\), where \(W\) is the filter, and \(k\) is half of the width of the filter.
Sobel filter: \(W_{x} = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}\) and \(W_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}\).
Image gradient: \(\nabla_{x} X = W_{x} \star X\), \(\nabla_{y} X = W_{y} \star X\), with gradient magnitude \(G = \sqrt{\nabla_{x}^{2} + \nabla_{y}^{2}}\) and gradient direction \(\Theta = arctan\left(\dfrac{\nabla_{y}}{\nabla_{x}}\right)\).
Convolution layer: \(A = g\left(W \star X + b\right)\), where \(A\) is the activation map.
Pooling layer: (max-pooling) \(a = \displaystyle\max\left\{x_{1}, ..., x_{m}\right\}\), (average-pooling) \(a = \dfrac{1}{m} \displaystyle\sum_{j=1}^{m} x_{j}\).
# Summary
📗 Tuesday to Friday lectures: 1:00 to 2:15, Zoom Link
📗 Saturday review sessions: 5:30 to 8:30, Zoom Link
📗 Personal meeting room: always open, Zoom Link
📗 Quiz (use your wisc ID to log in (without "@wisc.edu")): Socrative Link
📗 Math Homework:
M2,
M3,
M4,
M5,
M6,
M7,
📗 Programming Homework:
P1,
P2,
P3,
📗 Examples and Quizzes:
Q1,
Q2,
Q3,
Q4,
Q5,
Q6,
Q7,
Q8,
Q9,
Q10,
Q11,
Q12,
Q13,
Q14,
# Lectures
📗 Slides (before lecture, usually updated on Sunday):
Blank Slides:
Part 1,
Part 2,
Blank Slides (with blank pages for quiz questions): Part 1, Part 2,
📗 Slides (after lecture, usually updated on Friday):
Blank Slides with Quiz Questions:
Part 1,
Part 2,
Annotated Slides: Part 1, Part 2,
📗 Review Session:
PDF. Saturday: PDF.
📗 My handwriting is really bad, you should copy down your notes from the lecture videos instead of using these.
📗 Notes

Image by scikit learn
# Midterm Statistics
Exam M1A: Mean = 70.84%, Stdev = 19.49| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| MAX | 4 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 3 | 4 | 2 | 1 |
| PROB | 0.27 | 0.67 | 0.51 | 0.63 | 0.65 | 0.69 | 0.80 | 0.94 | 0.80 | 0.69 | 0.65 | 0.88 | 0.80 | 0.94 | 1 |
| RPBI | 2.73 | 5.25 | 4.26 | 5.07 | 5.17 | 5.32 | 7.11 | 4.93 | 5.33 | 5.32 | 6.89 | 4.75 | 7.11 | 2.47 | 0 |
Exam M2A: Mean = 74.43%, Stdev = 21.66
| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| MAX | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 3 | 4 | 4 | 3 | 4 | 1 |
| PROB | 0.51 | 0.82 | 0.45 | 0.71 | 0.88 | 0.96 | 0.73 | 0.76 | 0.71 | 0.84 | 0.84 | 0.75 | 0.82 | 0.63 | 1 |
| RPBI | 3.53 | 4.35 | 3.11 | 4.45 | 4.70 | 3.44 | 5.98 | 5.99 | 5.94 | 4.25 | 5.40 | 6 | 4.35 | 5.60 | 0 |
Exam MB: Mean = 65.07%, Stdev = 29.1
| Q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| MAX | 0 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 4 | 2 | 4 | 4 | 4 | 2 | 3 | 2 | 4 | 3 | 3 | 4 | 3 | 2 | 1 |
| PROB | 0 | 0.10 | 0.20 | 0.40 | 0.50 | 0.30 | 0.50 | 0.60 | 0.30 | 0.50 | 0.20 | 0.30 | 0.70 | 0.20 | 0.90 | 0.70 | 0.70 | 0.50 | 0.30 | 0.90 | 0.80 | 0.70 | 0.40 | 0.90 | 0.90 | 0.60 | 0.80 | 0.60 | 0.30 | 1 |
| RPBI | 0 | 0.04 | 0.12 | 0.29 | 0.37 | 0.21 | 0.37 | 0.44 | 0.16 | 0.37 | 0.12 | 0.21 | 0.48 | 0.12 | 0.25 | 0.64 | 0.32 | 0.50 | 0.27 | 0.42 | 0.32 | 0.48 | 0.20 | 0.48 | 0.40 | 0.44 | 0.64 | 0.44 | 0.14 | 0 |
PROB is the percentage of students who get this question correct.
RPBI is the (point biserial) correlation between getting this question correct with the total grade on the exam.
PROB < 0.25 or RPBI < 0 means this question is probably not well-made.
# Summary
📗 Coverage: supervised learning + reinforcement learning W1 to W4.
📗 Number of questions: 30
📗 Length: 2 x 1 hour 30 minutes
📗 Regular: July 26 AND July 27, 1:00 to 2:30 PM
📗 Make-up: July 27, 5:30 to 8:30 PM
📗 Link to relevant pages:
W1 : M2 and M3 W2 : M4 and M5
W3 : M6 and M7
Practice: X1 and X2 and X3 and X6
# Details
📗 Slides:
(1) The slides subtitled "Definition" and "Quiz" contain the mathematics and statistics that you are required to know for the exams. (2) The slides subtitled "Motivation" and "Discussion" contain concepts you should be familiar with, but the specific mathematics will not be tested on the exam.
(3) The slides subtitled "Description" and "Algorithm" are mostly useful for programming homework, not exams.
(4) The slides subtitled "Admin" are not relevant to the course materials.
📗 Questions:
(1) Around a third of the questions will be exactly the same as the homework questions (different randomization of parameters), you can practice by solving these homework again with someone else's ID (auto-grading will not work if you do not enter an ID). (2) Around a third of the questions will be similar to the past exam or quiz questions (ones that are covered during the lectures), going over the quiz questions will help, and solving the past exam questions will help.
(3) Around a third of the questions will be new, mostly from topics not covered in the homework, reading the slides will be helpful.
📗 Question types:
All questions will ask you to enter a number, vector (or list of options), or matrix. There will be no drawing or selecting objects on a canvas, and no text entry or essay questions. You will not get the hints like the ones in the homework. You can type your answers in a text file directly and submit it on Canvas. If you use the website, you can use the "calculate" button to make sure the expression you entered can be evaluated correctly when graded. You will receive 0 for incorrect answers and not-evaluate-able expressions, no partial marks, and no additional penalty for incorrect answers. # Other Materials
📗 Videos Going through Past Exam Questions
X1Q1-3 (Perceptrons): Link X1Q4-8 (SVMs): Link
X1Q9-10 (Kernels): Link
X1Q11-15 (KNN): Link
X2Q1-3 (Entropy): Link
X2Q4-6 (Decision Trees): Link
X2Q7-8 (Convolutions): Link
X2Q9-11 (CNNs): Link
X2Q12-15 (Probability): Link
X3Q1-3 (CPTs): Link
X3Q4-8 (Bayesian Networks): Link
📗 Pre-recorded Videos from 2020
Lecture 13 (Reinforcement Learning): Guest Lecture (see Canvas Zoom recording) Lecture 14 (Optimization): Guest Lecture (see Canvas Zoom recording)
📗 Relevant websites
2024 Online and In-Person Exams: EX1: Link
CX1: Link
CX2: Link
2023 Online Exams:
M1A: Link
M2A: Link
M1B: Link
M2B: Link
2022 Online Exams:
M1A-C: Link
M2A-C: Link
MB-C: Link
MA-E: Link
MB-E: Link
2021 Online Exams:
M1A-C: Link
M1B-C: Link
M2A-C: Link
M2B-C: Link
2020 Online Exams:
M1A-C: Link
M1B-C: Link
M2A-C: Link
M2B-C: Link
M1A-E: Link
M1B-E: Link
M2A-E: Link
M2B-E: Link
2019 In-person Exams:
Midterm Version A: Link
Version A Answers: ABEDE ECDDC CCBCC CEDBB CEECD DDDBC DBBAA AAADC
Midterm Version B: Link
Version B Answers: CCABD DAECE BCADC CCEBA DDCCD DDCCA AADBC ABDAB
Sample midterm: Link
📗 YouTube videos from 2019 and 2020
M2Q5: Link M3Q6: Link
M4Q3: Link
M4Q6: Link
M4Q8: Link
M5Q8: Link
M6Q1: Link
M6Q4: Link
M7Q1: Link
M7Q4: Link
HMM: Link
Other Midterm Questions
Q2 (KNN Decision Boundary Question): Link
Q3 (KNN Leave-One-Out Question): Link
Q4 (CNN Count Weights Question): Link
Q5 (Naive Bayes Count CPTs Question): Link
Q7 (Please do NOT forget to submit your homework on Canvas! Question): Link
# Keywords and Notations
📗 Supervised Learning:
Training item: \(\left(x_{i}, y_{i}\right)\), where \(i \in \left\{1, 2, ..., n\right\}\) is the instance index, \(x_{ij}\) is the feature \(j\) of instance \(i\), \(j \in \left\{1, 2, ..., m\right\}\) is the feature index, \(x_{i} = \left(x_{i1}, x_{i2}, ...., x_{im}\right)\) is the feature vector of instance \(i\), and \(y_{i}\) is the true label of instance \(i\). Test item: \(\left(x', y'\right)\), where \(j \in \left\{1, 2, ..., m\right\}\) is the feature index.
📗 Linear Threshold Unit, Linear Perceptron:
LTU Classifier: \(\hat{y}_{i} = 1_{\left\{w^\top x_{i} + b \geq 0\right\}}\), where \(w = \left(w_{1}, w_{2}, ..., w_{m}\right)\) is the weights, \(b\) is the bias, \(x_{i} = \left(x_{i1}, x_{i2}, ..., x_{im}\right)\) is the feature vector of instance \(i\), and \(\hat{y}_{i}\) is the predicted label of instance \(i\). Perceptron algorithm update step: \(w = w - \alpha \left(a_{i} - y_{i}\right) x_{i}\), \(b = b - \alpha \left(a_{i} - y_{i}\right)\), \(a_{i} = 1_{\left\{w^\top x_{i} + b \geq 0\right\}}\), where \(a_{i}\) is the activation value of instance \(i\).
📗 Loss Function:
Zero-one loss minimization: \(\hat{f} = \mathop{\mathrm{argmin}}_{f \in \mathcal{H}} \displaystyle\sum_{i=1}^{n} 1_{\left\{f\left(x_{i}\right) \neq y_{i}\right\}}\), where \(\hat{f}\) is the optimal classifier, \(\mathcal{H}\) is the hypothesis space (set of functions to choose from). Squared loss minimization of perceptrons: \(\left(\hat{w}, \hat{b}\right) = \mathop{\mathrm{argmin}}_{w, b} \dfrac{1}{2} \displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)^{2}\), \(a_{i} = g\left(w^\top x_{i} + b\right)\), where \(\hat{w}\) is the optimal weights, \(\hat{b}\) is the optimal bias, \(g\) is the activation function.
📗 Logistic Regression:
Logistic regression classifier: \(\hat{y}_{i} = 1_{\left\{a_{i} \geq 0.5\right\}}\), \(a_{i} = \dfrac{1}{1 + \exp\left(- \left(w^\top x_{i} + b\right)\right)}\). Loss minimization problem: \(\left(\hat{w}, \hat{b}\right) = \mathop{\mathrm{argmin}}_{w, b} -\displaystyle\sum_{i=1}^{n} \left(y_{i} \log\left(a_{i}\right) + \left(1 - y_{i}\right) \log\left(1 - a_{i}\right)\right)\), \(a_{i} = \dfrac{1}{1 + \exp\left(- \left(w^\top x_{i} + b\right)\right)}\).
Batch gradient descrent step: \(w = w - \alpha \displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right) x_{i}\), \(b = b - \alpha \displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)\), \(a_{i} = \dfrac{1}{1 + \exp\left(- \left(w^\top x_{i} + b\right)\right)}\), where \(\alpha\) is the learning rate.
📗 Neural Network:
Neural network classifier for two layer network with logistic activation: \(\hat{y}_{i} = 1_{\left\{a^{\left(2\right)}_{i} \geq 0.5\right\}}\) \(a^{\left(1\right)}_{ij} = \dfrac{1}{1 + \exp\left(- \left(\left(\displaystyle\sum_{j'=1}^{m} x_{ij'} w^{\left(1\right)}_{j'j}\right) + b^{\left(1\right)}_{j}\right)\right)}\), where \(m\) is the number of features (or input units), \(w^{\left(1\right)}_{j' j}\) is the layer \(1\) weight from input unit \(j'\) to hidden layer unit \(j\), \(b^{\left(1\right)}_{j}\) is the bias for hidden layer unit \(j\), \(a_{ij}^{\left(1\right)}\) is the layer \(1\) activation of instance \(i\) hidden unit \(j\).
\(a^{\left(2\right)}_{i} = \dfrac{1}{1 + \exp\left(- \left(\left(\displaystyle\sum_{j=1}^{h} a^{\left(1\right)}_{ij} w^{\left(2\right)}_{j}\right) + b^{\left(2\right)}\right)\right)}\), where \(h\) is the number of hidden units, \(w^{\left(2\right)}_{j}\) is the layer \(2\) weight from hidden layer unit \(j\), \(b^{\left(2\right)}\) is the bias for the output unit, \(a^{\left(2\right)}_{i}\) is the layer \(2\) activation of instance \(i\).
Stochastic gradient descent step for two layer network with squared loss and logistic activation:
\(w^{\left(1\right)}_{j' j} = w^{\left(1\right)}_{j' j} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right) w_{j}^{\left(2\right)} a_{ij}^{\left(1\right)} \left(1 - a_{ij}^{\left(1\right)}\right) x_{ij'}\).
\(b^{\left(1\right)}_{j} \leftarrow b^{\left(1\right)}_{j} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right) w_{j}^{\left(2\right)} a_{ij}^{\left(1\right)} \left(1 - a_{ij}^{\left(1\right)}\right)\).
\(w^{\left(2\right)}_{j} \leftarrow w^{\left(2\right)}_{j} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right) a_{ij}^{\left(1\right)}\).
\(b^{\left(2\right)} \leftarrow b^{\left(2\right)} - \alpha \left(a^{\left(2\right)}_{i} - y_{i}\right) a^{\left(2\right)}_{i} \left(1 - a^{\left(2\right)}_{i}\right)\).
📗 Multiple Classes:
Softmax activation for one layer networks: \(a_{ij} = \dfrac{\exp\left(- \left(w_{k^\top} x_{i} + b_{k}\right)\right)}{\displaystyle\sum_{k' = 1}^{K} \exp\left(- \left(w_{k'}^\top x_{i} + b_{k'}\right)\right)}\), where \(K\) is the number of classes (number of possible labels), \(a_{i k}\) is the activation of the output unit \(k\) for instance \(i\), \(y_{i k}\) is component \(k\) of the one-hot encoding of the label for instance \(i\). 📗 Regularization:
L1 regularization (squared loss): \(\displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)^{2} + \lambda \left(\displaystyle\sum_{j=1}^{m} \left| w_{j} \right| + \left| b \right|\right)\), where \(\lambda\) is the regularization parameter. L2 regularization (sqaured loss): \(\displaystyle\sum_{i=1}^{n} \left(a_{i} - y_{i}\right)^{2} + \lambda \left(\displaystyle\sum_{j=1}^{m} \left(w_{j}\right)^{2} + b^{2}\right)\).
📗 Support Vector Machine
SVM classifier: \(\hat{y}_{i} = 1_{\left\{w^\top x_{i} + b \geq 0\right\}}\). Hard margin, original max-margin formulation: \(\displaystyle\max_{w} \dfrac{2}{\sqrt{w^\top w}}\) such that \(w^\top x_{i} + b \leq -1\) if \(y_{i} = 0\) and \(w^\top x_{i} + b \geq 1\) if \(y_{i} = 1\).
Hard margin, simplified formulation: \(\displaystyle\min_{w} \dfrac{1}{2} w^\top w\) such that \(\left(2 y_{i} - 1\right)\left(w^\top x_{i} + b\right) \geq 1\).
Soft margin, original max-margin formulation: \(\displaystyle\min_{w} \dfrac{1}{2} w^\top w + \dfrac{1}{\lambda} \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \xi_{i}\) such that \(\left(2 y_{i} - 1\right)\left(w^\top x_{i} + b\right) \geq 1 - \xi, \xi \geq 0\), where \(\xi_{i}\) is the slack variable for instance \(i\), \(\lambda\) is the regularization parameter.
Soft margin, simplified formulation: \(\displaystyle\min_{w} \dfrac{\lambda}{2} w^\top w + \dfrac{1}{n} \displaystyle\sum_{i=1}^{n} \displaystyle\max\left\{0, 1 - \left(2 y_{i} - 1\right) \left(w^\top x_{i} + b\right)\right\}\)
Subgradient descent formula: \(w = \left(1 - \lambda\right) w - \alpha \left(2 y_{i} - 1\right) 1_{\left\{\left(2 y_{i} - 1\right) \left(w^\top x_{i} + b\right) \geq 1\right\}} x_{i}\).
📗 Kernel Trick
Kernel SVM classifier: \(\hat{y}_{i} = 1_{\left\{w^\top \varphi\left(x_{i}\right) + b \geq 0\right\}}\), where \(\varphi\) is the feature map. Kernal Gram matrix: \(K_{i i'} = \varphi\left(x_{i}\right)^\top \varphi\left(x_{i'}\right)\).
Quadratic Kernel: \(K_{i i'} = \left(x_{i^\top} x_{i'} + 1\right)^{2}\) has feature representation \(\varphi\left(x_{i}\right) = \left(x_{i1}^{2}, x_{i2}^{2}, \sqrt{2} x_{i1} x_{i2}, \sqrt{2} x_{i1}, \sqrt{2} x_{i2}, 1\right)\).
Gaussian RBF Kernel: \(K_{i i'} = \exp\left(- \dfrac{1}{2 \sigma^{2}} \left(x_{i} - x_{i'}\right)^\top \left(x_{i} - x_{i'}\right)\right)\) has infinite-dimensional feature representation, where \(\sigma^{2}\) is the variance parameter.
📗 Information Theory:
Entropy: \(H\left(Y\right) = -\displaystyle\sum_{y=1}^{K} p_{y} \log_{2} \left(p_{y}\right)\), where \(K\) is the number of classes (number of possible labels), \(p_{y}\) is the fraction of data points with label \(y\). Conditional entropy: \(H\left(Y | X\right) = -\displaystyle\sum_{x=1}^{K_{X}} p_{x} \displaystyle\sum_{y=1}^{K} p_{y|x} \log_{2} \left(p_{y|x}\right)\), where \(K_{X}\) is the number of possible values of feature, \(p_{x}\) is the fraction of data points with feature \(x\), \(p_{y|x}\) is the fraction of data points with label \(y\) among the ones with feature \(x\).
Information gain, for feature \(j\): \(I\left(Y | X_{j}\right) = H\left(Y\right) - H\left(Y | X_{j}\right)\).
📗 Decision Tree:
Decision stump classifier: \(\hat{y}_{i} = 1_{\left\{x_{ij} \geq t_{j}\right\}}\), where \(t_{j}\) is the threshold for feature \(j\). Feature selection: \(j^\star = \mathop{\mathrm{argmax}}_{j} I\left(Y | X_{j}\right)\).
📗 K-Nearest Neighbor:
Distance: (Euclidean) \(\rho\left(x, x'\right) = \left\|x - x'\right\|_{2} = \sqrt{\displaystyle\sum_{j=1}^{m} \left(x_{j} - x'_{j}\right)^{2}}\), (Manhattan) \(\rho\left(x, x'\right) = \left\|x - x'\right\|_{1} = \displaystyle\sum_{j=1}^{m} \left| x_{j} - x'_{j} \right|\), where \(x, x'\) are two instances. K-Nearest Neighbor classifier: \(\hat{y}_{i}\) = mode \(\left\{y_{\left(1\right)}, y_{\left(2\right)}, ..., y_{\left(k\right)}\right\}\), where mode is the majority label and \(y_{\left(t\right)}\) is the label of the \(t\)-th closest instance to instance \(i\) from the training set.
📗 Natural Language Processing:
Unigram model: \(\mathbb{P}\left\{z_{1}, z_{2}, ..., z_{d}\right\} = \displaystyle\prod_{t=1}^{d} \mathbb{P}\left\{z_{t}\right\}\) where \(z_{t}\) is the \(t\)-th token in a training item, and \(d\) is the total number of tokens in the item. Maximum likelihood estimator (unigram): \(\hat{\mathbb{P}}\left\{z_{t}\right\} = \dfrac{c_{z_{t}}}{\displaystyle\sum_{z=1}^{m} c_{z}}\), where \(c_{z}\) is the number of time the token \(z\) appears in the training set and \(m\) is the vocabulary size (number of unique tokens).
Maximum likelihood estimator (unigram, with Laplace smoothing): \(\hat{\mathbb{P}}\left\{z_{t}\right\} = \dfrac{c_{z_{t}} + 1}{\left(\displaystyle\sum_{z=1}^{m} c_{z}\right) + m}\).
Bigram model: \(\mathbb{P}\left\{z_{1}, z_{2}, ..., z_{d}\right\} = \mathbb{P}\left\{z_{1}\right\} \displaystyle\prod_{t=2}^{d} \mathbb{P}\left\{z_{t} | z_{t-1}\right\}\).
Maximum likelihood estimator (bigram): \(\hat{\mathbb{P}}\left\{z_{t} | z_{t-1}\right\} = \dfrac{c_{z_{t-1}, z_{t}}}{c_{z_{t-1}}}\).
Maximum likelihood estimator (bigram, with Laplace smoothing): \(\hat{\mathbb{P}}\left\{z_{t} | z_{t-1}\right\} = \dfrac{c_{z_{t-1}, z_{t}} + 1}{c_{z_{t-1}} + m}\).
📗 Probability Review:
Conditional probability: \(\mathbb{P}\left\{Y = y | X = x\right\} = \dfrac{\mathbb{P}\left\{Y = y, X = x\right\}}{\mathbb{P}\left\{X = x\right\}}\). Joint probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y \in Y} \mathbb{P}\left\{X = x, Y = y\right\}\).
Bayes rule: \(\mathbb{P}\left\{Y = y | X = x\right\} = \dfrac{\mathbb{P}\left\{X = x | Y = y\right\} \mathbb{P}\left\{Y = y\right\}}{\displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}}\).
Law of total probability: \(\mathbb{P}\left\{X = x\right\} = \displaystyle\sum_{y' \in Y} \mathbb{P}\left\{X = x | Y = y'\right\} \mathbb{P}\left\{Y = y'\right\}\).
Independence: \(X, Y\) are independent if \(\mathbb{P}\left\{X = x, Y = y\right\} = \mathbb{P}\left\{X = x\right\} \mathbb{P}\left\{Y = y\right\}\) for every \(x, y\).
Conditional independence: \(X, Y\) are conditionally independent conditioned on \(Z\) if \(\mathbb{P}\left\{X = x, Y = y | Z = z\right\} = \mathbb{P}\left\{X = x | Z = z\right\} \mathbb{P}\left\{Y = y | Z = z\right\}\) for every \(x, y, z\).
📗 Bayesian Network
Conditional Probability Table estimation: \(\hat{\mathbb{P}}\left\{x_{j} | p\left(X_{j}\right)\right\} = \dfrac{c_{x_{j}, p\left(X_{j}\right)}}{c_{p\left(X_{j}\right)}}\), where \(p\left(X_{j}\right)\) is the list of parents of \(X_{j}\) in the network. Conditional Probability Table estimation (with Laplace smoothing): \(\hat{\mathbb{P}}\left\{x_{j} | p\left(X_{j}\right)\right\} = \dfrac{c_{x_{j}, p\left(X_{j}\right)} + 1}{c_{p\left(X_{j}\right)} + \left| X_{j} \right|}\), where \(\left| X_{j} \right|\) is the number of possible values of \(X_{j}\).
Bayesian network inference: \(\mathbb{P}\left\{x_{1}, x_{2}, ..., x_{m}\right\} = \displaystyle\prod_{j=1}^{m} \mathbb{P}\left\{x_{j} | p\left(X_{j}\right)\right\}\).
Naive Bayes estimation: .
Naive Bayes classifier: \(\hat{y}_{i} = \mathop{\mathrm{argmax}}_{y} \mathbb{P}\left\{Y = y | X = X_{i}\right\}\).
📗 Convolution
Convolution (1D): \(a = x \star w\), \(a_{j} = \displaystyle\sum_{t=-k}^{k} w_{t} x_{j-t}\), where \(w\) is the filter, and \(k\) is half of the width of the filter. Convolution (2D): \(A = X \star W\), \(A_{j j'} = \displaystyle\sum_{s=-k}^{k} \displaystyle\sum_{t=-k}^{k} W_{s,t} X_{j-s,j'-t}\), where \(W\) is the filter, and \(k\) is half of the width of the filter.
Sobel filter: \(W_{x} = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}\) and \(W_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}\).
Image gradient: \(\nabla_{x} X = W_{x} \star X\), \(\nabla_{y} X = W_{y} \star X\), with gradient magnitude \(G = \sqrt{\nabla_{x}^{2} + \nabla_{y}^{2}}\) and gradient direction \(\Theta = arctan\left(\dfrac{\nabla_{y}}{\nabla_{x}}\right)\).
📗 Convolutional Neural Network
Fully connected layer: \(a = g\left(w^\top x + b\right)\), where \(a\) is the activation unit, \(g\) is the activation function. Convolution layer: \(A = g\left(W \star X + b\right)\), where \(A\) is the activation map.
Pooling layer: (max-pooling) \(a = \displaystyle\max\left\{x_{1}, ..., x_{m}\right\}\), (average-pooling) \(a = \dfrac{1}{m} \displaystyle\sum_{j=1}^{m} x_{j}\).
Last Updated: November 21, 2025 at 11:40 PM